I used a combination of spaces and replacements , but it gets out of hand quickly.
There must be added a feature for this IN THE NEXT MATHEMATICA VERSION FFS !!!
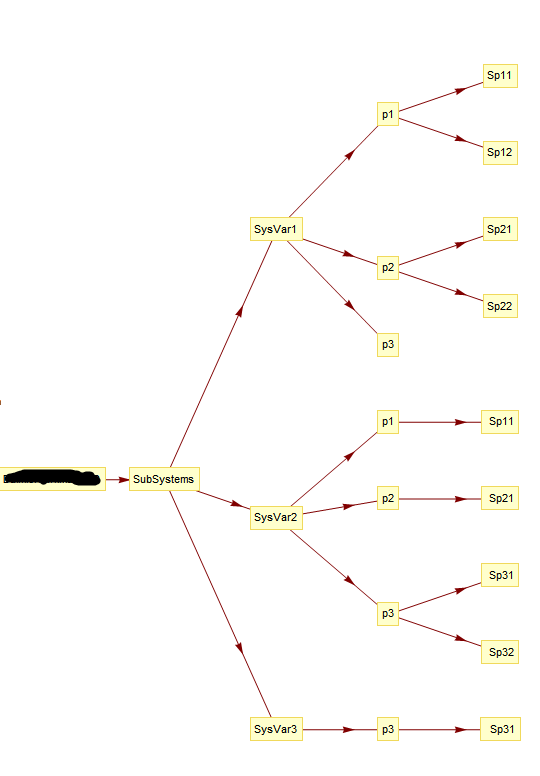
listNodesSubsystemView = Join[{ "XXX" -> "SubSystems"},
Reverse[{"SubSystems" -> "SysVar1", "SubSystems" -> "SysVar2",
"SubSystems" -> "SysVar3"}],
Reverse[
{"SysVar1" -> "p1S1", "SysVar1" -> "p2S1", "SysVar1" -> "p3S1",
"SysVar2" -> "p1S2", "SysVar2" -> "p2S2", "SysVar2" -> "p3S2",
"SysVar3" -> "p3S3"}],
Reverse[{"p1S1" -> "Sp11", "p1S1" -> "Sp12", "p2S1" -> "Sp21",
"p2S1" -> "Sp22",(*in system variant S1*)
"p1S2" -> " Sp11", "p2S2" -> " Sp21", "p3S2" -> " Sp31",
"p3S2" -> " Sp32",(*in system variant S2*)
"p3S3" -> " Sp31"}]];(*in system variant S3*)
TreeSubSystem =
TreePlot[listNodesSubsystemView, Left,
First[ First[listNodesSubsystemView]], VertexLabeling -> True,
DirectedEdges -> True] /. "p2S1" | "p2S2" | "p2S3" -> "p2" /.
"p3S1" | "p3S2" | "p3S3" -> "p3" /.
"p1S1" | "p1S2" | "p1S3" -> "p1";