Message Boards

WOLFRAM COMMUNITY

9878 Views

7 Replies

0 Total Likes

View groups...

Follow this post

Share this post:

GROUPS:

Mathematics Equation Solving Wolfram Language

solve for highly nonlinear double variable, decoupled equation

Palas Kar

Posted 10 years ago

In[29]= h = 6.62610^-34; q = 1.610^-19; k = 1.3810^-23; c = 310^8; ts = 6000; fw = 2.1810^-5; te = 300; ms = (kts); me = (kte); vol2 = (qv2)/(kte); vol1 = (qv1)/(kte); Eg1 = Input[] Eg2 = Input[] nu1ts = (Eg1q)/(kts); nu2ts = (Eg2q)/(kts); nu1te = (Eg1q)/(kte); nu2te = (Eg2q)/(kte); qi1te = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu1te, Infinity}]; qs1te = (qi1te2\[Pi](me^3))/((h^3)(c^2)) f01 = 2qs1te; i01 = qf01; qi2te = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu2te, Infinity}]; qs2te = (qi2te2\[Pi](me^3))/((h^3)(c^2)) f02 = 2qs2te; i02 = qf02; qi1ts = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu1ts, Infinity}]; qs1ts = (qi1ts2\[Pi](ms^3))/((h^3)(c^2)) qi12ts = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu2ts, nu1ts}] qs12ts = (qi12ts2\[Pi](ms^3))/((h^3)(c^2)) (fs1=(fwqs1ts)+(qs1teExp[vol2]) fs2=(fwqs12ts)+(qs1teExp[vol1])) NSolve[{(1 + vol1) Exp[vol1] - ((((fwqs1ts) + (qs1teExp[vol2]))/f01)) - (.5vol2 Exp[vol1]) == 0, (1 + vol2)* Exp[vol2] - ((((fwqs12ts) + (qs1teExp[vol1]))/ f02)) - ((qs1te/qs2te).5vol1Exp[vol2]) == 0}, {vol1, vol2}] take Eg1=1.7 and Eg2=1.12 NSolve::ivar: 38.6473 v1 is not a valid variable. >> NSolve[{-225.314 (2.1838310^21 + 0.00221913 E^(38.6473 v2)) + E^(38.6473 v1) (1 + 38.6473 v1) - 19.3237 E^(38.6473 v1) v2 == 0, -9.4080110^-8 (1.7261410^21 + 0.00221913 E^(38.6473 v1)) - 8.0686310^-9 E^(38.6473 v2) v1 + E^(38.6473 v2) (1 + 38.6473 v2) == 0}, {38.6473 v1, 38.6473 v2}] but does not give any solution for v1 and v2 Attachments:*

In[29]= h = 6.626*10^-34;    
    q = 1.6*10^-19;    
    k = 1.38*10^-23;   
    c = 3*10^8;   
    ts = 6000;   
    fw = 2.18*10^-5;   
    te = 300;   
    ms = (k*ts);     
    me = (k*te);   
    vol2 = (q*v2)/(k*te);   
    vol1 = (q*v1)/(k*te);     
    Eg1 = Input[]       
    Eg2 = Input[]          
    nu1ts = (Eg1*q)/(k*ts);   
    nu2ts = (Eg2*q)/(k*ts);   
    nu1te = (Eg1*q)/(k*te);    
    nu2te = (Eg2*q)/(k*te);    
    qi1te = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu1te, Infinity}];           
    qs1te = (qi1te*2*\[Pi]*(me^3))/((h^3)*(c^2))       
    f01 = 2*qs1te;      
    i01 = q*f01;         
    qi2te = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu2te, Infinity}];        
    qs2te = (qi2te*2*\[Pi]*(me^3))/((h^3)*(c^2))        
    f02 = 2*qs2te;        
    i02 = q*f02;          
    qi1ts = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu1ts, Infinity}];            
    qs1ts = (qi1ts*2*\[Pi]*(ms^3))/((h^3)*(c^2))       
    qi12ts = NIntegrate[(x^2)/(-1 + (Exp[x])), {x, nu2ts, nu1ts}]        
    qs12ts = (qi12ts*2*\[Pi]*(ms^3))/((h^3)*(c^2))          
    (*fs1=(fw*qs1ts)+(qs1te*Exp[vol2])            
    fs2=(fw*qs12ts)+(qs1te*Exp[vol1])*)           
    NSolve[{(1 + vol1)*
         Exp[vol1] - ((((fw*qs1ts) + (qs1te*Exp[vol2]))/f01)) - (.5*vol2*
          Exp[vol1]) == 
       0, (1 + vol2)*
         Exp[vol2] - ((((fw*qs12ts) + (qs1te*Exp[vol1]))/
           f02)) - ((qs1te/qs2te)*.5*vol1*Exp[vol2]) == 0}, {vol1, vol2}]             

    take Eg1=1.7       
    and Eg2=1.12       
    NSolve::ivar: 38.6473 v1 is not a valid variable. >>          
    NSolve[{-225.314 (2.18383*10^21 + 0.00221913 E^(38.6473 v2)) + 
        E^(38.6473 v1) (1 + 38.6473 v1) - 19.3237 E^(38.6473 v1) v2 == 
       0, -9.40801*10^-8 (1.72614*10^21 + 0.00221913 E^(38.6473 v1)) - 
        8.06863*10^-9 E^(38.6473 v2) v1 + 
        E^(38.6473 v2) (1 + 38.6473 v2) == 0}, {38.6473 v1, 38.6473 v2}]

but does not give any solution for v1 and v2

POSTED BY: Palas Kar

7 Replies

Sort By:

Bill Simpson

Posted 10 years ago

Many changes in this and you must verify that all those are correct and why each character was changed. In[1]:= h = 6.62610^-34; q = 1.610^-19; k = 1.3810^-23; c = 310^8; ts = 6000; fw = 2.1810^-5; te = 300; ms = kts; me = kte; vol2 = qv2/(kte); vol1 = qv1/(kte); Eg1 = Input[]; Eg2 = Input[]; nu1ts = Eg1q/(kts); nu2ts = Eg2q/(kts); nu1te = Eg1q/(kte); nu2te = Eg2q/(kte); qi1te = NIntegrate[x^2/(-1 + Exp[x]), {x, nu1te, Infinity}]; qs1te = qi1te 2 \[Pi] me^3/(h^3 c^2); f01 = 2 qs1te; i01 = qf01; qi2te = NIntegrate[x^2/(-1 + Exp[x]), {x, nu2te, Infinity}]; qs2te = qi2te 2 \[Pi] me^3/(h^3 c^2); f02 = 2 qs2te; i02 = qf02; qi1ts = NIntegrate[x^2/(-1 + Exp[x]), {x, nu1ts, Infinity}]; qs1ts = qi1ts 2 \[Pi] ms^3/(h^3 c^2); qi12ts = NIntegrate[x^2/(-1 + Exp[x]), {x, nu2ts, nu1ts}]; qs12ts = qi12ts 2 \[Pi] ms^3/(h^3 c^2); fs1 = fwqs1ts + qs1teExp[vol2]; fs2 = fwqs12ts + qs1teExp[vol1]; FindRoot[{(1 + vol1) Exp[vol1] - (fwqs1ts + qs1teExp[vol2])/f01 - .5 vol2 Exp[vol1] == 0, (1 + vol2) Exp[vol2] - (fwqs12ts + qs1teExp[vol1])/f02 - qs1te/qs2te .5 vol1*Exp[vol2] == 0}, {{v1, 1000}, {v2, 1000}}] Out[32]= {v1 -> 4998.29, v2 -> 3300.01}

Many changes in this and you must verify that all those are correct and why each character was changed.

In[1]:= h = 6.62610^-34;
q = 1.610^-19;
k = 1.3810^-23;
c = 310^8;
ts = 6000;
fw = 2.1810^-5;
te = 300;
ms = k*ts;
me = k*te;
vol2 = q*v2/(k*te);
vol1 = q*v1/(k*te);
Eg1 = Input[];
Eg2 = Input[];
nu1ts = Eg1*q/(k*ts);
nu2ts = Eg2*q/(k*ts);
nu1te = Eg1*q/(k*te);
nu2te = Eg2*q/(k*te);
qi1te = NIntegrate[x^2/(-1 + Exp[x]), {x, nu1te, Infinity}];
qs1te = qi1te 2 \[Pi] me^3/(h^3 c^2);
f01 = 2 qs1te;
i01 = q*f01;
qi2te = NIntegrate[x^2/(-1 + Exp[x]), {x, nu2te, Infinity}];
qs2te = qi2te 2 \[Pi] me^3/(h^3 c^2);
f02 = 2 qs2te;
i02 = q*f02;
qi1ts = NIntegrate[x^2/(-1 + Exp[x]), {x, nu1ts, Infinity}];
qs1ts = qi1ts 2 \[Pi] ms^3/(h^3 c^2);
qi12ts = NIntegrate[x^2/(-1 + Exp[x]), {x, nu2ts, nu1ts}];
qs12ts = qi12ts 2 \[Pi] ms^3/(h^3 c^2);
fs1 = fw*qs1ts + qs1te*Exp[vol2];
 fs2 = fw*qs12ts + qs1te*Exp[vol1];
FindRoot[{(1 + vol1) Exp[vol1] - (fw*qs1ts + qs1te*Exp[vol2])/f01 - .5 vol2 Exp[vol1] == 0,
   (1 + vol2) Exp[vol2] - (fw*qs12ts + qs1te*Exp[vol1])/f02 - qs1te/qs2te .5 vol1*Exp[vol2] == 0},
   {{v1, 1000}, {v2, 1000}}]    

Out[32]= {v1 -> 4998.29, v2 -> 3300.01}

POSTED BY: Bill Simpson

Palas Kar

Posted 10 years ago

Expected v1 in the range of 1 to 3 volt. And v2 0.1 to 1.5 volt. the error message is " FindRoot::cvmit: Failed to converge to the requested accuracy or precision within 100 iterations. >> "

POSTED BY: Palas Kar

Jim Baldwin

Jim Baldwin, Retired

Posted 10 years ago

The code from Bill Simpson works fine for me (Windows 7, Mathematica 10.0) (i.e., no errors with the same results). Contour plots of the resulting equations in the rectangular area for v1 (1 to 3) and v2 (0.1 to 1.5) does not give any values near zero. ContourPlot[(1 + vol1) Exp[vol1] - (fwqs1ts + qs1teExp[vol2])/ f01 - .5 vol2 Exp[vol1], {v1, 1, 3}, {v2, .1, 1.5}, ContourLabels -> All, ContourShading -> None, Frame -> True, FrameLabel -> {{Style["v2", Large], ""}, {Style["v1", Large], ""}}] ContourPlot[(1 + vol2) Exp[vol2] - (fwqs12ts + qs1teExp[vol1])/f02 - qs1te/qs2te .5 vol1*Exp[vol2], {v1, 1, 3}, {v2, .1, 1.5}, ContourLabels -> All, ContourShading -> None, Frame -> True, FrameLabel -> {{Style["v2", Large], ""}, {Style["v1", Large], ""}}] 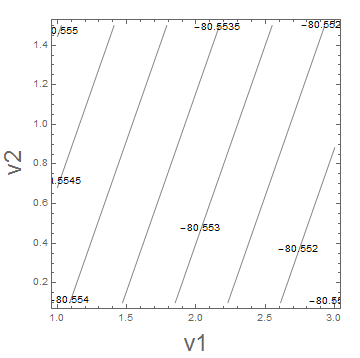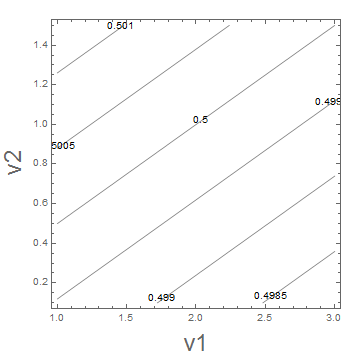So it would seem there are 4 somewhat overlapping possbilities: (1) there is some different in Bill's translation, (2) the original code is not exactly what is desired, (3) the thought that v1 and v2 should be in the stated ranges is wrong, and (4) the code is correct and the results for v1 and v2 are correct. Do you have other possibilities that you'll be checking out?

POSTED BY: Jim Baldwin

Bill Simpson

Posted 10 years ago

Perhaps he was looking for vol1 and vol2 from the calculated values of v1 and v2. Those are much closer to his estimates.

POSTED BY: Bill Simpson

Palas Kar

Posted 10 years ago

what is the value of vol1 and vol2?

POSTED BY: Palas Kar

Bill Simpson

Posted 10 years ago

Usual syntax for using results from Solve, FindRoot, etc. for further calculations. In[1]:= <<<snip>>> sol = FindRoot[{(1 + vol1) Exp[vol1] - (fwqs1ts + qs1teExp[vol2])/f01 - .5 vol2 Exp[vol1] == 0, (1 + vol2) Exp[vol2] - (fwqs12ts + qs1teExp[vol1])/f02 - qs1te/qs2te .5 vol1Exp[vol2] == 0}, {{v1, 1000}, {v2, 1000}}] Out[32]= {v1 -> 4998.29, v2 -> 3300.01} In[33]:= {qv1/(kte), qv2/(k*te)} /. sol Out[33]= {3.28446, 2.16849}

Usual syntax for using results from Solve, FindRoot, etc. for further calculations.

In[1]:= <<<snip>>>
sol = FindRoot[{(1 + vol1) Exp[vol1] - (fw*qs1ts + qs1te*Exp[vol2])/f01 - .5 vol2 Exp[vol1] == 0,
   (1 + vol2) Exp[vol2] - (fw*qs12ts + qs1te*Exp[vol1])/f02 - qs1te/qs2te .5 vol1*Exp[vol2] == 0}, {{v1, 1000}, {v2, 1000}}]

Out[32]= {v1 -> 4998.29, v2 -> 3300.01}

In[33]:= {q*v1/(k*te), q*v2/(k*te)} /. sol

Out[33]= {3.28446, 2.16849}

POSTED BY: Bill Simpson

Palas Kar

Posted 10 years ago

please find the attachment.... here I explain my problem in detail............. Attachments:

POSTED BY: Palas Kar

Reply to this discussion

Reply Preview

Attachments

Remove Add a file to this post

Follow this discussion

or Discard

Group Abstract

Feedback