I like to study x^(1/x) as much as possible, because of two reasons. One is the MRB constant an alternating sum of all positive integers to the power of their reciprocal. The second is the following which is true only for a certain small range! A number, n, taken to the power of itself an infinite number of times found by solving for x in x^(1/x)==n. For example what is 2/10 to itself an infinite number of times? You could compute it through brute force by entering
In[294]:= N[Nest[Power[2/10, #] &, 1, 100], 30]
Out[294]= 0.469621922935881329117128363349,
Or, to get a much more accurate solution by using x^(1/x), you could enter
In[295]:= FindRoot[x^(1/x) - 2/10, {x, .46}, WorkingPrecision -> 30]
Out[295]= {x -> 0.469621922935610544117803066891}.
Nonetheless, here is what I wanted to say:
Considering f(x)=x^(1/x) for the range [-1,0), when does the Im(f)==Re(f)? You might be surprised to find out, it is at rational values of x.
Plot[Im[x^(1/x)] - Re[x^(1/x)], {x, -1, 0}]
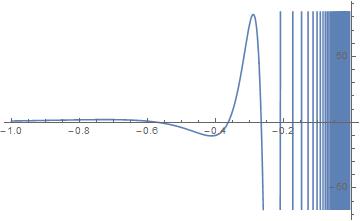
Where on the graph does Im[x^(1/x)] - Re[x^(1/x)]==0?
I used FindRoot to find a few of them:
In[222]:= FindRoot[{Im[x^(1/x)] == Re[x^(1/x)]}, {x, -.6},
WorkingPrecision -> 100]
Out[222]= {x -> \
-0.5714285714285714285714285714285714285714285714285714285714285714285\
714285714285714285714285714285714}
In[299]:= N[-4/7, 100]
Out[299]= \
-0.5714285714285714285714285714285714285714285714285714285714285714285\
714285714285714285714285714285714
In[229]:= FindRoot[{Im[x^(1/x)] == Re[x^(1/x)]}, {x, -.4},
WorkingPrecision -> 100]
Out[229]= {x -> \
-0.3636363636363636363636363636363636363636363636363636363636363636363\
636363636363636363636363636363635}
In[300]:= N[-4/11, 100]
Out[300]= \
-0.3636363636363636363636363636363636363636363636363636363636363636363\
636363636363636363636363636363636
In[233]:= FindRoot[{Im[x^(1/x)] == Re[x^(1/x)]}, {x, -.2},
WorkingPrecision -> 100]
Out[233]= {x -> \
-0.2105263157894736842105263157894736842105263157894736842105263157894\
736842105263157894736842105263158}
In[301]:= N[-4/19, 100]
Out[301]= \
-0.2105263157894736842105263157894736842105263157894736842105263157894\
736842105263157894736842105263158
Notice, we found Im[x^(1/x)] == Re[x^(1/x)] at -4 over some (but not all) primes.
In[269]:= FullSimplify[
Table[{p = -4/Prime[x], Im[p^(1/p)] == Re[p^(1/p)]}, {x, 1, 10}]]
Out[269]= {{-2, False}, {-(4/3), True}, {-(4/5), False}, {-(4/7),
True}, {-(4/11), True}, {-(4/13), False}, {-(4/17),
False}, {-(4/19), True}, {-(4/23), True}, {-(4/29), False}}
I then found several of such primes: I haven't figured the pattern out for the primes, though.
In[265]:= FullSimplify[
Table[{p = -4/Prime[x],
Im[p^(1/p)] == Re[p^(1/p)]}, {x, {2, 4, 5, 8, 9, 11, 14, 15, 17,
19, 20, 22, 23, 27, 28, 31, 32, 34, 36, 38, 39, 41, 43, 46, 47,
48, 49, 52, 54, 56, 58, 61, 63, 64, 67, 69, 72, 73, 75, 76, 81,
83, 85, 86, 90, 91, 92, 93, 94, 95, 96, 99}}]]
Out[265]= {{-(4/3), True}, {-(4/7), True}, {-(4/11), True}, {-(4/19),
True}, {-(4/23), True}, {-(4/31), True}, {-(4/43), True}, {-(4/47),
True}, {-(4/59), True}, {-(4/67), True}, {-(4/71), True}, {-(4/79),
True}, {-(4/83), True}, {-(4/103), True}, {-(4/107),
True}, {-(4/127), True}, {-(4/131), True}, {-(4/139),
True}, {-(4/151), True}, {-(4/163), True}, {-(4/167),
True}, {-(4/179), True}, {-(4/191), True}, {-(4/199),
True}, {-(4/211), True}, {-(4/223), True}, {-(4/227),
True}, {-(4/239), True}, {-(4/251), True}, {-(4/263),
True}, {-(4/271), True}, {-(4/283), True}, {-(4/307),
True}, {-(4/311), True}, {-(4/331), True}, {-(4/347),
True}, {-(4/359), True}, {-(4/367), True}, {-(4/379),
True}, {-(4/383), True}, {-(4/419), True}, {-(4/431),
True}, {-(4/439), True}, {-(4/443), True}, {-(4/463),
True}, {-(4/467), True}, {-(4/479), True}, {-(4/487),
True}, {-(4/491), True}, {-(4/499), True}, {-(4/503),
True}, {-(4/523), True}}
We need to figure out the pattern for {2, 4, 5, 8, 9, 11, 14, 15, 17, 19, 20, 22, 23, 27, 28, 31, 32, 34, 36, 38, 39, 41, 43, 46, 47, 48, 49, 52, 54, 56, 58, 61, 63, 64, 67, 69, 72, 73, 75, 76, 81, 83, 85, 86, 90, 91, 92, 93, 94, 95, 96, 99... . Then, whether we will have found all values for x where Im(f)==Re(f) in [-1,0),may still an open question. However, we will have found a countable infinitude of them that are rational! I posted a notebook with all of this information in it.
 Attachments:
Attachments: