Just a note:

triplets[[;;, 3]] = Rescale @ triplets[[;;, 3]]

will be faster.

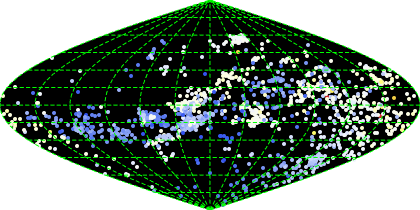
To add to Jose's response, if you want to color the points different colors efficiently, you can redefine p as follows (there may be a shorter way, but this works):

p = With[{triples = 
    Cases[rad, {a_, b_, c_?NumberQ} :> {b, Mod[a, 360, -180], c}]}, 
  triples /. {a_, b_, c_} :> {a, b, 
     Rescale[c, {Min[triples[[All, 3]]], Max[triples[[All, 3]]]}]}];

Then, you can generate colors for each of the triples:

colors = ColorData["TemperatureMap"][#] & /@ p[[All, 3]];

The colors can be efficiently applied using VertexColors on the Point primitive:

GeoGraphics[{PointSize[0.01], 
  Point[GeoPosition[p[[All, 1 ;; 2]]], VertexColors -> colors]}, 
 GeoRange -> All, GeoProjection -> "Sinusoidal", 
 GeoGridLines -> Automatic, 
 GeoGridLinesStyle -> Directive[Dashing[{.01, .005}], Green], 
 GeoBackground -> Black]

Starting from your proposed solution I would suggest the following simplification. A single GeoGraphics can produce the desired output and handles everything related to the projection. In version 10.0.2 GeoProjectionData also has the "Hammer" (or Hammer-Aitoff) and "Aitoff" projections.

rad = Import["~/Downloads/DadosRad2014_RADECVELOC_15124_1024.dat"];
p = Cases[rad, {a_, b_, c_} -> {b, Mod[a, 360, -180]}];

GeoGraphics[{Red, PointSize[0.01], Point[GeoPosition[p]]}, 
 GeoRange -> All, GeoProjection -> "Sinusoidal", 
 GeoGridLines -> Automatic, GeoGridLinesStyle -> Directive[Dashing[{.01, .005}], Green], 
 GeoBackground -> Black
]