Here is an old piece of code from many years ago that does something similar:
circlesOnCircles[?_, ?_, ?_, iter_] :=
Module[{C, ?, cp, \[ScriptD], ?, ?},
C[?[mp_, r_, {?_, ?_}, -1, i_]] :=
(cp = mp + r (\[ScriptD] = {Cos[?], Sin[?]});
? = ?.{r, 1/i}; ? = ?.{? - ?, i};
{?[cp + \[ScriptD] ?, ?, {? - Pi - ?, ? - Pi}, 1, i + 1],
?[cp - \[ScriptD] ?, ?, {?, ? + ?}, -1, i + 1]});
C[?[mp_, r_, {?_, ?_}, 1, i_]] :=
(cp = mp + r (\[ScriptD] = {Cos[?], Sin[?]});
? = ?.{r, 1/i}; ? = ?.{? - ?, i};
{?[cp + \[ScriptD] ?, ?, {? - Pi, ? - Pi + ?}, -1, i + 1],
?[cp - \[ScriptD] ?, ?, {? - ?, ?}, 1, i + 1]});
Graphics[#, PlotRange -> All]& @
{Flatten[MapIndexed[{Thickness[0.01/#2[[1]]], Circle @@ Take[#,3]&/@#}&,
NestList[Flatten[C /@ #]&,
Join[?[{0, 0}, 1, ?{-1, 1} Pi/2, #, 1]& /@ {-1, 1},
?[{2, 0}, 1, Pi + ?{-1, 1} Pi/2, #, 1]& /@ {-1, 1}], iter]]]}]
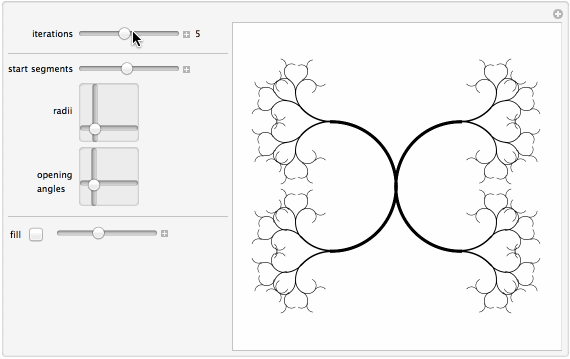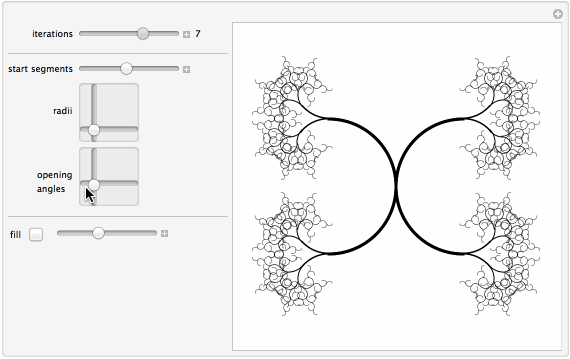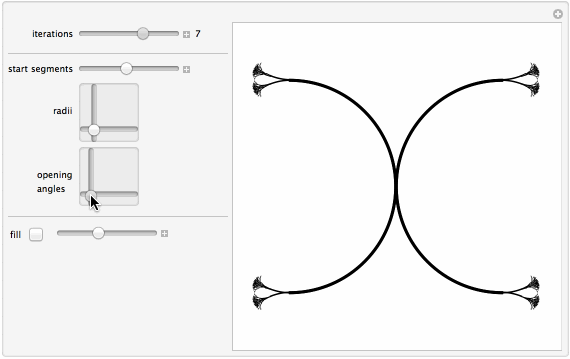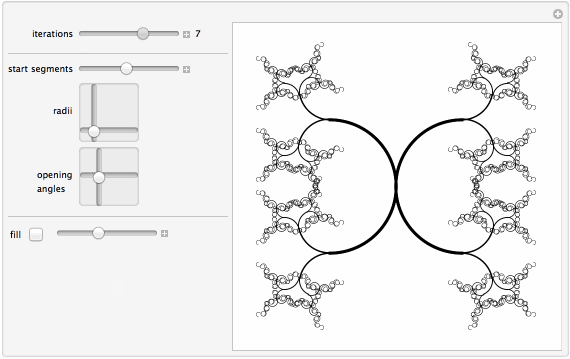
Manipulate[
circlesOnCircles[?, ?, ?, iter] /.
If[dcq, c_Circle :> {Opacity[op], Disk @@ c}, {}],
{{iter, 5, "iterations"}, 1, 10, 1, ImageSize -> Small,
Appearance -> "Labeled"},
Delimiter,
{{?, 1, "start segments"}, 0.1, 2,
ImageSize -> Small},
{{?, {0.37, 0.25}, "radii"}, {0, 0}, {2, 2},
ImageSize -> Small},
{{?, {0.17, 0.31}, "opening\nangles"}, {0, 0}, {1,
1}, ImageSize -> Small},
Delimiter,
Row[{Control[{{dcq, False, "fill"}, {True, False}}], " ",
Control[{{op, 0.4, ""}, 0, 1, ImageSize -> Small}]}],
ControlPlacement -> Left]
 Attachments:
Attachments: