There is a pole at x=0 (the integrand is infinity at 0)
Limit[x^3*BesselK[2, x] BesselK[2, x], x -> 0]
(*infinity*)
You can also see this by writing
Clear[a]
Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, a, Infinity}]
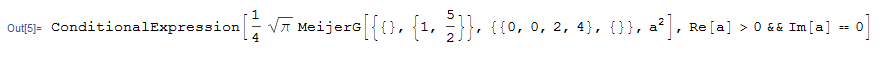
Notice the Re[a]>0 in the above.
Now, why GenerateConditions -> False made it work? I do not know. I think this is a bug. But I am no expert on this. I do not think the value generated is even correct. Compare
Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 0, Infinity}, GenerateConditions -> False] // N
(*.797059*)
to
Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 10^(-64), Infinity}] // N
(*590.259*)
Compare also what happens when using PrincipalValue -> True which tells it to ignore the simple pole at x=0
Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 0, Infinity}, PrincipalValue -> True]
it returns unevaluated. So I have no idea where this result
Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 0, Infinity}, GenerateConditions -> False]
(*1/3 - 4 EulerGamma + Log[16]*)
came from.