Thanks for your answer.

Have you noticed that the result of the forth line just equals to 1/3 - 4 EulerGamma + Log[16] ?

How I find this?Using the following code.

Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, m, Infinity}]/ Log[m] /. m -> 10^-16 // N

the answer is (-4.02163).(Of cousre,if you change 10^-16 to 10^-64,you'll get -4.00541).

It shows that the integral and Log[m] are infinites of the same order when m=0.

I'm a rookie on this.I'm wondering that "GenerateConditions -> False" can eliminate the divergent terms automatically.I do not know.

For further check.I have do the integral of x,x^2,x^-1,Log[x],and so on,which are obviously divergent. But "GenerateConditions -> False" makes them equal to zero.

Integrate[x, {x, 0, Infinity},GenerateConditions -> False]

Thanks again.

There is a pole at x=0 (the integrand is infinity at 0)

    Limit[x^3*BesselK[2, x] BesselK[2, x], x -> 0]
    (*infinity*)

You can also see this by writing

Clear[a]
Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, a, Infinity}]

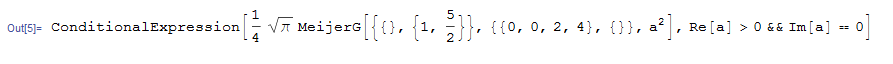
Notice the Re[a]>0 in the above.

Now, why GenerateConditions -> False made it work? I do not know. I think this is a bug. But I am no expert on this. I do not think the value generated is even correct. Compare

Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 0, Infinity}, GenerateConditions -> False] // N
(*.797059*)

to

    Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 10^(-64), Infinity}] // N
    (*590.259*)

Compare also what happens when using PrincipalValue -> True which tells it to ignore the simple pole at x=0

       Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 0, Infinity}, PrincipalValue -> True]

it returns unevaluated. So I have no idea where this result

        Integrate[x^3*BesselK[2, x] BesselK[2, x], {x, 0, Infinity}, GenerateConditions -> False]
        (*1/3 - 4 EulerGamma + Log[16]*)

came from.