Well, you could look for the interval for which all the conditions on x and y are fulfilled. This can be done like so:

Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 &&x >= 0 && y >= 0, {x, y}]

You get

(0 <= x <= 40 && 0 <= y <= (480 - x)/4) || (40 < x <= 70 && 0 <= y <= 150 - x) || (70 < x <= 90 && 0 <= y <= 220 - 2 x)

You can get z

Solve[z == 100 x + 200 y  && (Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 && x >= 0 && y >= 0, {x, y}]), z, Reals]

which gives:

{{z -> ConditionalExpression[100 x + 200 y, (0 < x < 90 && 0 < y < 40) || (x > 0 && 40 < y < 80 && -220 + 2 x + y < 0) || (x > 0 && 80 < y < 110 &&x + y < 150) || (x > 0 && 110 < y < 120 && x + 4 y < 480)]}}

If you want to maximize z you might want to look into expressions like:

Maximize[100 x + 200 y , (Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 && x >= 0 && y >= 0, {x, y}]), {x, y}]

which finds:

{26000, {x -> 40, y -> 110}}

If you feel like it, you can also plot the whole thing:

Show[Plot3D[100 x + 200 y, {x, 0, 200}, {y, 0, 200}, 
  RegionFunction -> 
   Function[{x, y, z}, 
    Evaluate[
     Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && 
        x <= 90 && x >= 0 && y >= 0, {x, y}][[1]]]]], 
 Plot3D[100 x + 200 y, {x, 0, 200}, {y, 0, 200}, 
  RegionFunction -> 
   Function[{x, y, z}, 
    Evaluate[
     Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && 
        x <= 90 && x >= 0 && y >= 0, {x, y}][[2]]]]], 
 Plot3D[100 x + 200 y, {x, 0, 200}, {y, 0, 200}, 
  RegionFunction -> 
   Function[{x, y, z}, 
    Evaluate[
     Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && 
        x <= 90 && x >= 0 && y >= 0, {x, y}][[3]]]]]]

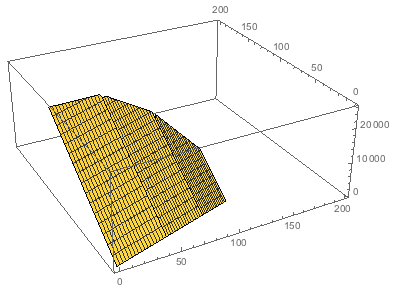
If you minimize the expression:

Minimize[100 x + 200 y , (Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 && x >= 0 && y >= 0, {x, y}]), {x, y}]

you find

{0, {x -> 0, y -> 0}

so it appears that z can take values between 0 and 26000.

Cheers,

Marco