Well, you could look for the interval for which all the conditions on x and y are fulfilled. This can be done like so:
Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 &&x >= 0 && y >= 0, {x, y}]
You get
(0 <= x <= 40 && 0 <= y <= (480 - x)/4) || (40 < x <= 70 && 0 <= y <= 150 - x) || (70 < x <= 90 && 0 <= y <= 220 - 2 x)
You can get z
Solve[z == 100 x + 200 y && (Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 && x >= 0 && y >= 0, {x, y}]), z, Reals]
which gives:
{{z -> ConditionalExpression[100 x + 200 y, (0 < x < 90 && 0 < y < 40) || (x > 0 && 40 < y < 80 && -220 + 2 x + y < 0) || (x > 0 && 80 < y < 110 &&x + y < 150) || (x > 0 && 110 < y < 120 && x + 4 y < 480)]}}
If you want to maximize z you might want to look into expressions like:
Maximize[100 x + 200 y , (Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 && x >= 0 && y >= 0, {x, y}]), {x, y}]
which finds:
{26000, {x -> 40, y -> 110}}
If you feel like it, you can also plot the whole thing:
Show[Plot3D[100 x + 200 y, {x, 0, 200}, {y, 0, 200},
RegionFunction ->
Function[{x, y, z},
Evaluate[
Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 &&
x <= 90 && x >= 0 && y >= 0, {x, y}][[1]]]]],
Plot3D[100 x + 200 y, {x, 0, 200}, {y, 0, 200},
RegionFunction ->
Function[{x, y, z},
Evaluate[
Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 &&
x <= 90 && x >= 0 && y >= 0, {x, y}][[2]]]]],
Plot3D[100 x + 200 y, {x, 0, 200}, {y, 0, 200},
RegionFunction ->
Function[{x, y, z},
Evaluate[
Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 &&
x <= 90 && x >= 0 && y >= 0, {x, y}][[3]]]]]]
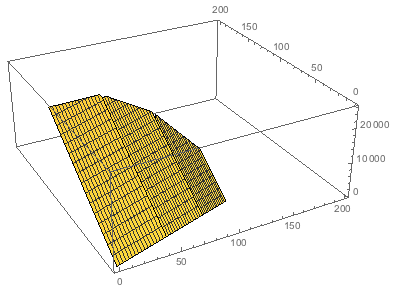
If you minimize the expression:
Minimize[100 x + 200 y , (Reduce[4 x + 2 y <= 440 && x + 4 y <= 480 && x + y <= 150 && x <= 90 && x >= 0 && y >= 0, {x, y}]), {x, y}]
you find
{0, {x -> 0, y -> 0}
so it appears that z can take values between 0 and 26000.
Cheers,
Marco