Dear Intan,
I guess that I would need more information, on what exactly the problem is. The figure in the attached pptx document does not help.
In Maximize or NMaximize tend to work in 3D example. Let's look at:
Plot3D[Cos[x^2 + y^2]*Exp[-0.3 (x^2 + y^2)], {x, -6, 6}, {y, -6, 6}, PlotRange -> All]
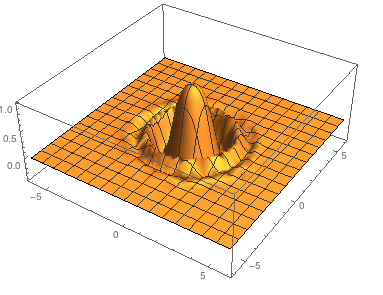
If you then simply use the Maximize function you get:
Maximize[{Cos[x^2 + y^2]*Exp[-0.3 (x^2 + y^2)] && -6 < x < 6 && -6 < y < 6}, {x, y}]
(*{1., {x -> -1.06836*10^-8, y -> -7.75192*10^-9}}*)
which says that the maximum value of 1 is reached at (numerically) {0,0}.
Cheers,
Marco