Hi Greg,
the integral evaluates to:
ConditionalExpression[
2.71828^(0.458675/c) c Hypergeometric2F1[-(1./c), -(1./c), 1. - 1./c, 0.367879] -
2.71828^(-0.541325/c) c Hypergeometric2F1[-(1./c), -(1./c), 1. - 1./c, 1.], Re[1/c] > -1.]
So suppose that Solve will not be able to find a non-numerical solution to your equation. If you plot the solution you find:
Plot[{Evaluate[2.718281828459045`^(0.4586751453870819`/c)
c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c,
0.36787944117144233`] -
2.718281828459045`^(-0.541324854612918`/c)
c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c, 1.`]],
0.5}, {c, 0.1, 1.7}]
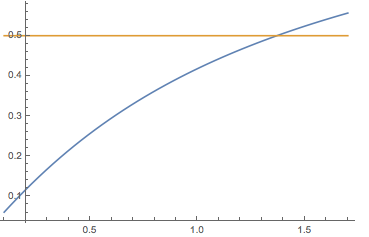
You can find the solution by
FindRoot[Evaluate[
1.` 2.718281828459045`^(0.4586751453870819`/c)
c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c,
0.36787944117144233`] -
1.` 2.718281828459045`^(-0.541324854612918`/c)
c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c, 1.`]] ==
0.5, {c, 1.4}]
this gives {c -> 1.36961}.
Cheers,
Marco