Hi Greg,

the integral evaluates to:

ConditionalExpression[
 2.71828^(0.458675/c) c Hypergeometric2F1[-(1./c), -(1./c), 1. - 1./c, 0.367879] - 
  2.71828^(-0.541325/c) c Hypergeometric2F1[-(1./c), -(1./c), 1. - 1./c, 1.], Re[1/c] > -1.]

So suppose that Solve will not be able to find a non-numerical solution to your equation. If you plot the solution you find:

Plot[{Evaluate[2.718281828459045`^(0.4586751453870819`/c)
      c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c, 
      0.36787944117144233`] - 
      2.718281828459045`^(-0.541324854612918`/c)
      c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c, 1.`]], 
  0.5}, {c, 0.1, 1.7}]

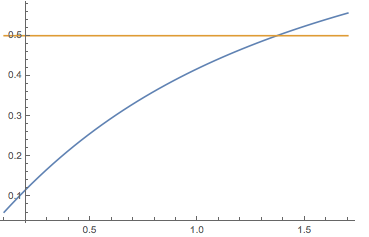
You can find the solution by

FindRoot[Evaluate[
   1.` 2.718281828459045`^(0.4586751453870819`/c)
      c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c, 
      0.36787944117144233`] - 
    1.` 2.718281828459045`^(-0.541324854612918`/c)
      c Hypergeometric2F1[-(1.`/c), -(1.`/c), 1.` - 1.`/c, 1.`]] == 
  0.5, {c, 1.4}]

this gives {c -> 1.36961}.

Cheers,

Marco