(The question has changed since the answer was posted.)

Hi,

is this a Mathematica question or a general Mathematics question?

The equation you give is clearly not in Mathematica format and we need to make several assumptions here to guess what you are looking for. Let's suppose that you are looking for a curve given in polar coordinates, where $r$ is the radius and $\Theta$ is the angle. We could then plot the curve

PolarPlot[Sqrt[Cos[theta]^2 + 1], {theta, 0, 2 Pi}, AspectRatio -> 1]

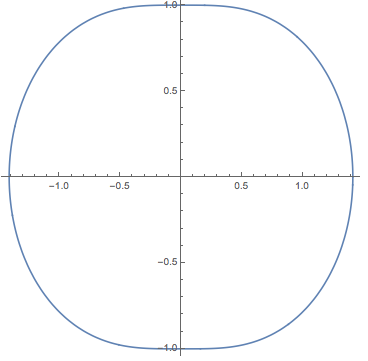
It does look somewhat nicer if you square the $\Theta$ only and not the $Cos$:

PolarPlot[Sqrt[Cos[theta^2] + 1], {theta, 0, 2 Pi}, AspectRatio -> 1]

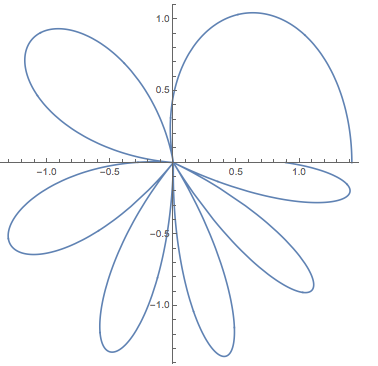
We can also rotate for more than $2 Pi$ and add a little color:

PolarPlot[Sqrt[Cos[theta^2] + 1], {theta, 0, 16 Pi}, AspectRatio -> 1,PlotPoints -> 500, ColorFunction -> Function[{x, y, t, r}, Hue[r]]]

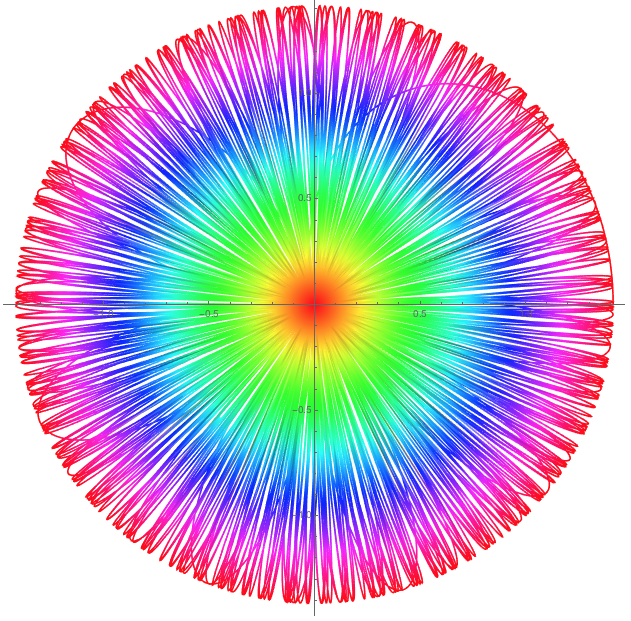
Well, there are lot's of things you can do with Mathematica. It is worthwhile to have a look at Mathematica. You can, of course, also just type your equation into Wolfram Alpha like so:

http://www.wolframalpha.com/input/?i=r%3D%3DSqrt%5BCos%5Btheta%5D%5E2%2B1%5D

That gives you a whole lot of information about that implicit function. Here are the first couple of lines from the output:

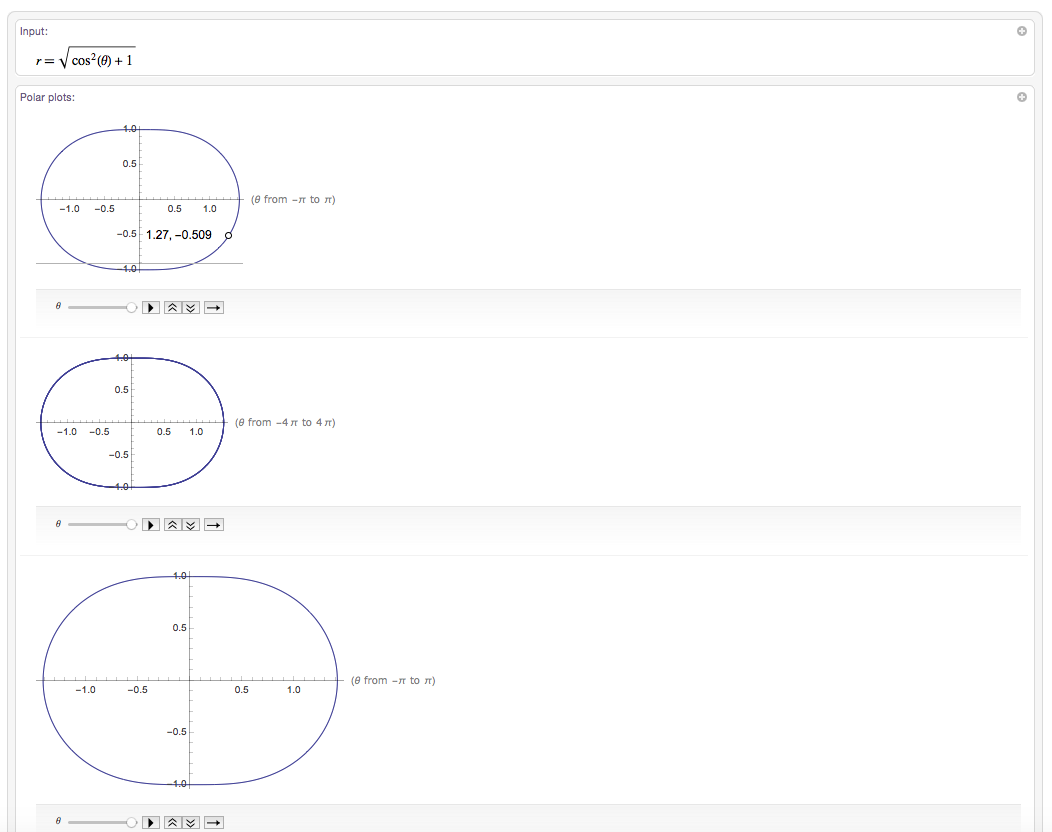
You even get sliders etc, to better study the equation.

Cheers,

M.

If you want the solution in cartesian coordinates, which now appears what you want, you can use:

TransformedField["Polar" -> "Cartesian", r == Sqrt[Cos[\[CapitalTheta]]^2 + 1], {r, \[Theta]} -> {x, y}]

(*Sqrt[x^2 + y^2] == Sqrt[1 + Cos[\[CapitalTheta]]^2]*)

That still contains the $Theta$ so you can use

TransformedField["Polar" -> "Cartesian", r == Sqrt[Cos[\[CapitalTheta]]^2 + 1], {r, \[Theta]} -> {x, y}] /. \[CapitalTheta] -> 
  CoordinateTransform["Cartesian" -> "Polar", {x, y}][[2]]//FullSimplify

(*x^2 + y^2 == 1 + x^2/(x^2 + y^2)*)

To convert that to the equation you desire, you can multiply both sides by $(x^2+y^2)$:

Map[#*(x^2 + y^2) &, %] // FullSimplify

(* (x^2 + y^2)^2 == 2 x^2 + y^2*)

Cheers,

M.