Hi,
I am not sure whether I am completely off topic here, because I ignore the part of "TraditionalForm", because I don't like typing like that, and it's not always quite clear. But if you want to implement the D'Alembert ratio test
f[a_] := Which[Limit[a[n + 1]/a[n], n -> Infinity] < 1, "convergent", Limit[a[n + 1]/a[n], n -> Infinity] > 1, "divergent", Limit[a[n+1]/a[n ], n -> Infinity] == 1, "indeterminate"];
does the trick. If you input a given sequence it tells you whether it converges or not:
c[n_] := 1/n;
f[c]
(*Indeterminate*)
Alternatively you can use pure functions:
f[1/#&]
(*Indeterminate*)
You can also use built in functions:
f[Fibonacci]
(*divergent*)
Of course, you also can see convergent ones like this one:
f[(1/2)^# &]
(*convergent*)
As I said, I do not like the TraditionalForm a lot, but if you want to see how the function looks you can use:
Which[Limit[a[n + 1]/a[n], n -> Infinity] < 1, "convergent", Limit[a[n + 1]/a[n], n -> Infinity] > 1, "divergent", Limit[a[n+1]/a[n ], n -> Infinity] == 1, "indeterminate"] // TraditionalForm
This gives:
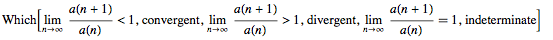
I am aware that this probably does not answer you question, but it does implement the D'Alembert ratio test.
Cheers,
Marco