Dean, I suspect that most of what's in the latest version is in Wikipedia.

BTW using the classroom assistant palette under Typesetting in the 5th row 4th entry you also find the standard brackets you need to do these statements. The result is this:

This looks like standard typesetting and works just fine:

v[2^-# &]

(*convergent*)

Cheers,

Marco

If you convert this to standard form it gives you yet another way of writing the same thing:

v[a_] := Piecewise[{
    {"convergent", Limit[a[n + 1]/a[n], n -> \[Infinity]] < 1}, 
    {"divergent", Limit[a[n + 1]/a[n], n -> \[Infinity]] > 1}, 
    {"indeterminate", Limit[a[n + 1]/a[n], n -> \[Infinity]] == 1}}]

Hi,

I am not sure whether I am completely off topic here, because I ignore the part of "TraditionalForm", because I don't like typing like that, and it's not always quite clear. But if you want to implement the D'Alembert ratio test

f[a_] := Which[Limit[a[n + 1]/a[n], n -> Infinity] < 1, "convergent", Limit[a[n + 1]/a[n], n -> Infinity] > 1, "divergent", Limit[a[n+1]/a[n ], n -> Infinity] == 1, "indeterminate"];

does the trick. If you input a given sequence it tells you whether it converges or not:

c[n_] := 1/n;
f[c]

(*Indeterminate*)

Alternatively you can use pure functions:

f[1/#&]

(*Indeterminate*)

You can also use built in functions:

f[Fibonacci]

(*divergent*)

Of course, you also can see convergent ones like this one:

f[(1/2)^# &]

(*convergent*)

As I said, I do not like the TraditionalForm a lot, but if you want to see how the function looks you can use:

Which[Limit[a[n + 1]/a[n], n -> Infinity] < 1, "convergent", Limit[a[n + 1]/a[n], n -> Infinity] > 1, "divergent", Limit[a[n+1]/a[n ], n -> Infinity] == 1, "indeterminate"] // TraditionalForm

This gives:

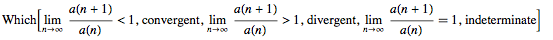
I am aware that this probably does not answer you question, but it does implement the D'Alembert ratio test.

Cheers,

Marco

In words, let a(n) be terms of an infinite series. If, in the limit as n approaches infinity, a(n+1)/a(n) < 1, then the series is convergent. Similarly if the ratio is > 1, then it is divergent. If the ratio = 1 however, then the test is inconclusive.

I just want to type this "pretty", like a textbook.

Thanks.

Apologies for the fury of replies to my little question. I've been trying (in vain) to find a picture or link to illustrate my point. The closest I can come is the following:

Suppose I'd like to type the alternate statement of D'Alembert's ratio test (see 1.6 in Mathematical Methods for Physicists by Arfken et al, 7th edition) in traditional form (i.e. the big left curly brace with conditions to the right). How can I do this in Mathematica?

Thanks,

Dean Sparrow

Thank you for your answer but this is a function, RSolve expects an equation, so I can not simply plug f into RSolve, do you see what I mean?

I have a related question. I have the following conditional equation:

f(n) =1+2 f(n/2) when n is even

f(n) = 1+f((n-1)/2)+f((n+1)/2) when n is odd

I want to represent this as a conditional equation to be used in RSolve with f(1)=1. How do I express this in Mathematica? If[cond,e1,e2] doesn't work.

Mathematica has an If function.