Message Boards Message Boards

0
|
10646 Views
|
9 Replies
|
9 Total Likes
View groups...
Share
Share this post:

Zero crossings and zero almost-crossings

Art Haan
Posted 10 years ago

I try to get to get a zero crossing of a complicated function, which has local minima, see figure repulsion above a superconductor.

If I use FindRoot of this function at zero, It does not find the crossing at 13 micron (as in the figure) but at 9.2 micron, which has a value close to zero. Why isn't there an Intersection algorithm for functions in Mathematica? NSolve is too slow and accuracygoal and precisiongoal does not help. Is there a way to get the intersection value with the zero line (zero crossing)??
POSTED BY: Art Haan
9 Replies
Sort By:

You might want to try the RootSearch package from Ted Ersek from the Wolfram Library Archive. I'm not certain if it still works in Version 10, but it was very good at finding roots of single parameter functions.

http://library.wolfram.com/infocenter/MathSource/4482/

POSTED BY: David J M Park Jr

FindRoot might work better if you multiply the function by 10^9
POSTED BY: Frank Kampas

It would help if you posted your code snippet
POSTED BY: Kay Herbert

Here is an example of Ted Ersek's RootSearch package that you can get from the Wolfram Library Archive. I did slightly modify his package so it's in an Ersek folder in my Applications folder. And I think I may have added several Quiet statements. 

<< Ersek`RootSearch`
f1[x_] := Sin[4 x] - (1 + x)/8;
Plot[f1[x], {x, -13, 12}]

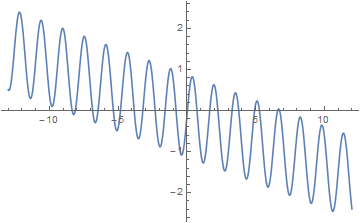
enter image description here

RootSearch[f1[x] == 0, {x, -13, 12}]

giving:

{{x -> -8.34829}, {x -> -8.12893}, {x -> -6.86295}, {x -> -6.47147}, 
{x -> -5.35392}, {x -> -4.83746}, {x -> -3.83638}, {x -> -3.21162}, 
{x -> -2.31492}, {x -> -1.58923}, {x -> -0.791902}, {x ->  0.0323512},
{x -> 0.730877}, {x -> 1.65538}, {x -> 2.25155}, {x -> 3.28282},
{x -> 3.76739}, {x -> 4.92069}, {x -> 5.27249}, {x -> 6.59611}, {x -> 6.73982}}

Ted's code will find all the roots within a specified range of the parameter. It even finds roots where the function just touches zero but doesn't cross it. Mathematica has many ways of finding roots, some of them based of algebraic methods or Solve or Reduce. But it lacks a simple 1-dimensional numerical search. Ted's program is very good at that.
POSTED BY: David J M Park Jr

But it lacks a simple 1-dimensional numerical search.

Because it's not simple. The simple search is known as Newton's method: 

In[32]:= nsZ[f_, x0_, n_Integer: 100] := If[NumericQ[f[x0]],
  FixedPoint[(# - f[#]/f'[#])&, N[x0], n], (* else *)
  Print["Function f = ", f, " is not numeric at x0 = ", x0];
  Return[$Failed]
  ]

In[40]:= Clear[f]
f[x_] := 3 (x - 1)^3 - (x + 1)^2 + x

a test function

it has in its naive form some problems (e.g. if it hits a local extremum by chance)

In[43]:= f /@ (nsZ[f, #]& /@ Range[0, 4])
Out[43]= {35.0768, 123.983, 7.02827*10^-7, 3.10862*10^-14, 0.0000145634}

but is easy to implement and very fast as long as evaluation of the function and it's derivative are fast.

Less naive, one could fold Newton's method first to find the extrema than the zeroes ...
POSTED BY: Udo Krause

Yes but Ted's RootSearch algorithm, based on the literature, is much more than a bare Newton's method. It finds all of the roots within a search range and it doesn't get thrown off if a Newton iteration is outside the search range. And it is simple to use. 

f[x_] := 3 (x - 1)^3 - (x + 1)^2 + x
RootSearch[f[x] == 0, {x, -1, 4}, PrecisionGoal -> 20]

giving:

{{x -> 2.4730512839991728510}}

This did not require a "good" starting point. No starting point was specified, only the search domain.
POSTED BY: David J M Park Jr
Art Haan
Art Haan
Posted 10 years ago

Thank you for the info, see attach for the code.

Attachments:
POSTED BY: Art Haan

Art,

Here is the solution using Ted Ersek's RootSearch package.

<< Ersek`RootSearch`
RootSearch[Ftot[x, 0, 5*^-6] + k0*(x - 7.53*^-6) == 0, {x, 0*^-6, 20*^-6}]

giving:

{{x -> 0.000012988}}
POSTED BY: David J M Park Jr

And here is the zero using the built-in FindRoot

In[24]:= FindRoot[Ftot[x, 0, 5 10^(-6)] + k0*(x - 7.53 10^(-6)) == 0, {x, 0}, 
                  WorkingPrecision -> 2 $MachinePrecision]
During evaluation of In[24]:= FindRoot::precw: The precision of the argument function (<<1>>==0) is less than WorkingPrecision (31.909179540382006`). >>
Out[24]= {x -> 0.000012988020154476412351028027555890}

In[25]:= $MachinePrecision
Out[25]= 15.9546

working in the nanometer range it is clear that usual WorkingPrecision is not enough (Frank Kampas intended to point that out with his post). Quite often Mathematica built-in functions work far better than their absent-minded usage seems to suggest.

The FindRoot::precw message can be avoided if the constants are given with the precision needed, with other words

In[32]:= FindRoot[
   SetPrecision[Ftot[x, 0, 5 10^(-6)] + k0*(x - 7.53 10^(-6)), #] == 0, {x, 0}, WorkingPrecision -> #] &[2 $MachinePrecision]
Out[32]= {x -> 0.000012988020154476412351028027555890}
POSTED BY: Udo Krause
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract