One of the growing known formulas for the MRB constant, here B, is 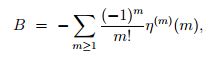
where you use consecutive mth Dirichlet eta derivatives of m. (I hope I said that right.)
Below etaMM[m, pr] is a module that rapidly computes the above mentioned Dirichlet eta derivatives of m for m>1 to "pr" decimals.
Clear[n];
etaMM[m_, pr_] :=
Module[{a, d, s, k, b, c}, a[j_] := Log[j + 1]^m/(j + 1)^m;
n = Floor[1.32 pr];
d = Cos[n ArcCos[3]];
{b, c, s} = {-1, -d, 0};
Do[c = b - c;
s = s + c a[k];
b = (k + n) (k - n) b/((k + 1) (k + 1/2)), {k, 0, n - 1}];
Return[N[s/d, pr] (-1)^m]];
When experimenting with etaMM it seemed that the limit etaMM(x)/etaMM(x+1) as x goes to infinity converged to -3/Log[3] as x grew large. So I entered the following.
Limit[etaMM[x, 30]/etaMM[x + 1, 30], x -> Infinity]
-2.730717679880512180842720
N[-3/Log[3], 30]
-2.73071767988051218084272049721
I then put my attention on the similar limit of etaMM(x)/etaMM(x+2) and entered,
Limit[etaMM[x, 30]/etaMM[x + 2, 30], x -> Infinity]
7.4568190472120073993794257
N[(-3/Log[3])^2, 30]
7.45681904721200739937942566098
I then looked to see if -3/Log[3])^n fit the pattern for the above mentioned limit of etaMM(x)/etaMM(x+n) by entering the following command.
Table[Limit[etaMM[x, 30 + n]/etaMM[x + n, 30 + n], x -> Infinity] -
N[(-3/Log[3])^n, 30], {n, 1, 10}]
{-1.37235287940800822169041524488*10^40,
2.79444910535423129879510807704*10^41, \
-7.63085157751707944108437643731*10^41,
2.08377013152699855184232233095*10^42, \
-4.24307018055104941251691654111*10^43,
1.15866267590045475709082282171*10^44, \
-3.16398065409903564894573215540*10^44,
6.44264535810872405469659678725*10^45, \
-1.75930455845876064949571024220*10^46, \
-1.31188157413621969593288955467*10^47}
Please join in the conversation if you have anything to add! In particular I would like to find a shortcut for finding etaMM(x+n) from etaMM(x). This may be hard to do because etaMM(x) is not at all well behaved for small x and works its way to near 0 for larger x.; see the following.
ListPlot[Table[etaMM[1 + x, 30], {x, 1, 10}]]
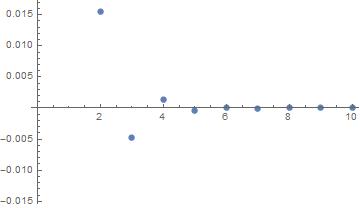
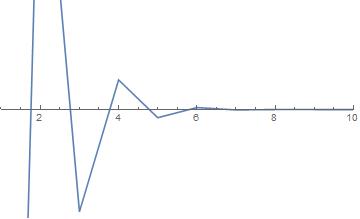
It is my guess that etaMM is a decaying, semi-oscillating function:
ListPlot[Table[etaMM[1 + x, 30], {x, 1, 10}],
PlotRange -> {{1, 10}, {-0.005, 0.005}}, Joined -> True]
Table[etaMM[1 + x, 30], {x, 1, 10}] // TableForm
