Hi Mike,
Let's not stop the integration -- we'll just accumulate a list of the positive crossings:
In[157]:= L = 2 Pi;
M = 1;
x = 35 Degree;
In[160]:= rLimit = 2.5; tList = {};
In[161]:= (* notice I used NDSolveValue to get o[t] and r[t] *)
{fo, fr} =
NDSolveValue[{r''[t] == -(4*Pi^2/r[t]^2) + ((o'[t]^2)*r[t]) +
HeavisideTheta[5 - t]*0.51*Cos[x],
o''[t] == (-2 r'[t]*o'[t])/r[t] +
HeavisideTheta[5 - t]*0.51*Sin[x], o[0] == 0, o'[0] == 2*Pi,
r[0] == 1, r'[0] == 0,
WhenEvent[r[t] >= rLimit, AppendTo[tList, {t, r[t]}]]}, {o[t],
r[t]}, {t, -10, 10}];
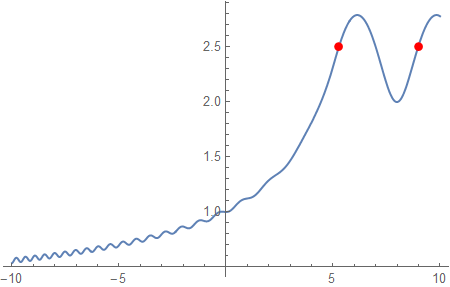
In[162]:= (* here are the positive crossings *)
tList
Out[162]= {{5.27189, 2.5}, {8.97694, 2.5}}
In[163]:= (* The first is of course at t = *)
tList[[1, 1]]
Out[163]= 5.27189
In[164]:= (* We can see them on the plot *)
Plot[fr, {t, -10, 10},
Epilog -> {Red, PointSize[Large], Point /@ tList}]
Regarding my earlier comment, I think tStop, or in this case tList, needs to be defined before its use in WhenEvent because that provides it with global scope. Otherwise it has scope local to NDSolve and expires when NDSolve finishes.
Best Regards,
David