Message Boards Message Boards

Doing a KenKen in Wolfram Language

Here's today's New York Times 4x4 KenKen solved in Mathematica. The approach is to first construct all possible arrays with different numbers in each row, from that select all arrays that have different numbers in each column, then apply the constraints on various cells. For this particular example, it was not necessary to apply all the constraints to get the unique answer. It is necessary to take the absolute value of some difference and ratio constraints, since it the order of the difference or ratio is not known.

Dimensions[p4 = Permutations[Range[4]]]

Out[1]= {24, 4}

Dimensions[a1 = Flatten[Outer[List, p4, p4, p4, p4, 1], 3]] 

Out[2]= {331776, 4, 4}

Dimensions[
 a2 = Select[
   a1, (And @@ (And @@ Unequal[Sequence @@ #] &) /@ Transpose[#]) &]] 

Out[3]= {576, 4, 4}

Dimensions[a3 = Select[a2, #[[1, 1]]*#[[1, 2]]*#[[2, 2]] == 12 &]]

Out[4]= {112, 4, 4}

Dimensions[a4 = Select[a3, Abs[Log[#[[1, 3]]/#[[1, 4]]]] == Log[2] &]]

Out[5]= {64, 4, 4}

In[6]:= Dimensions[
 a5 = Select[
   a4, #[[2, 1]] + #[[3, 1]] + #[[3, 2]] + #[[4, 1]] == 11 &]]

Out[6]= {8, 4, 4}

In[7]:= Dimensions[a6 = Select[a5, Abs[#[[2, 3]] - #[[3, 3]]] == 2 &]]

Out[7]= {6, 4, 4}

In[8]:= Dimensions[a7 = Select[a6, #[[2, 4]] == 2 &]]

Out[8]= {1, 4, 4}

In[10]:= a7

Out[10]= {{{1, 3, 2, 4}, {3, 4, 1, 2}, {4, 2, 3, 1}, {2, 1, 4, 3}}}
POSTED BY: Frank Kampas
20 Replies
Sort By:

I think that this is amazing code! :-)

I recently came across even more amazing code, in another language - APL. Sorry for the digression, but it solves KenKen in about 20 lines of insanely dense code. Here you go....

z?n fillcage x;t;o;c;k;f;m;at;z1;z2 ? we have to search and place the number t o c?x f?{|???,o,?} ? executes char operation in a function at?{a?(n×n)?0 ? a[(,?n n)??]?? ? n n?a} ? Places numbers ? in the cells ? k??¯1+?c :If o=' ' z??c at t :Else m?(?n)({??.f ?}?k)?n ? All possible combinations :If ~o='÷' z?c?at¨(t=,m)/,??m ? The coords of the cells that make the target # :Else z1?c?at¨(t=,m)/,??m ? For division we need to check the reciprocal too z2?c?at¨((÷t)=,m)/,??m z?z1,z2 :EndIf :EndIf

z?kenken x;n;sum n?0.5*????,/x[;3] ? dimension of the KenKen sum?{a?,??.+? ? f?{?/{{????}?~0}¨??} ? a/?(f¨?¨a)?f¨a} z???sum/n?fillcage¨?x
POSTED BY: Nick Brandaleone

I've been able to speed up my code for doing the 4x4 KenKen by doing it row at a time

In[1]:= n = 4;

In[2]:= rn = Range[n];

In[3]:= colUnequal[l_List] :=  
 Select[l, And @@ (UnsameQ  @@@ Transpose[#]) &]

In[4]:= addRow[l_List, p_List] := 
 Join[#[[1]], {#[[2]]}] & /@ Tuples[{l, p}]

In[5]:= Timing @ Dimensions[p = Permutations[rn]]

Out[5]= {0., {24, 4}}

In[6]:= Timing @ 
 Dimensions[ps = Select[p, Abs[Log[#[[3]]/#[[4]]]] == Log[2] &]]

Out[6]= {0., {8, 4}}

In[7]:= Timing @ Dimensions[a2 = Tuples[{ps, p}] ]

Out[7]= {0., {192, 2, 4}}

In[8]:= Timing @ Dimensions[a2s = colUnequal[a2]]

Out[8]= {0., {72, 2, 4}}

In[9]:= Timing @ Dimensions[a2s1 = Select[a2s, #[[2, 4]] == 2 &]] 

Out[9]= {0., {12, 2, 4}}

In[10]:= Timing @ 
 Dimensions[a2s2 = Select[a2s1, #[[1, 1]]*#[[1, 2]]*#[[2, 2]] == 12 &]]

Out[10]= {0., {4, 2, 4}}

In[11]:= Timing @ Dimensions[a3 = addRow[a2s2, p]]

Out[11]= {0., {96, 3, 4}}

In[12]:= Timing @ Dimensions[a3s = colUnequal[a3]]

Out[12]= {0., {8, 3, 4}}

In[13]:= Timing @ 
 Dimensions[a3s1 = Select[a3s, Abs[#[[2, 3]] - #[[3, 3]]] == 2 &]]

Out[13]= {0., {3, 3, 4}}

In[14]:= Timing @ Dimensions[a4 = addRow[a3s, p]]

Out[14]= {0., {192, 4, 4}}

In[15]:= Timing @ Dimensions[a4s = colUnequal[a4]]

Out[15]= {0., {8, 4, 4}}

In[16]:= Timing @ 
 Dimensions[
  a4s1 = Select[
    a4s, #[[2, 1]] + #[[3, 1]] + #[[3, 2]] + #[[4, 1]] == 11 &]]

Out[16]= {0., {1, 4, 4}}

In[17]:= a4s1[[1]]

Out[17]= {{1, 3, 2, 4}, {3, 4, 1, 2}, {4, 2, 3, 1}, {2, 1, 4, 3}}
POSTED BY: Frank Kampas

I haven't tried 6*6 grids with my approach as I suspect your approach is superior. I've also been wondering what's the best way to generate a Latin Square (different elements in all rows and columns) in Mathematica. I was thinking about starting with the upper left corner and then adding a row and a column element at a time, restricting the added value to be different from the other values its row and column, and then adding another row and column, etc.

POSTED BY: Frank Kampas

Not bad! 41 Megabytes! But it will be problematic for 6*6 grids or larger I'm afraid. Did you try to adapt your script to 6x6 grids?
POSTED BY: Sander Huisman 
In[1]:= MemoryInUse[]

Out[1]= 28876504

In[2]:= Timing @ Dimensions[p4 = Permutations[Range[4]]]

Out[2]= {0., {24, 4}}

In[3]:= MemoryInUse[]

Out[3]= 38100432

In[4]:= Timing @ Dimensions[a1 = Tuples[p4, 4]] 

Out[4]= {0.015625, {331776, 4, 4}}

In[5]:= MemoryInUse[]

Out[5]= 80572336

In[7]:= Timing @ Dimensions[a2 = Intersection[a1, Transpose /@ a1]]

Out[7]= {0.078125, {576, 4, 4}}

In[8]:= MemoryInUse[]

Out[8]= 80657696

In[9]:= Clear[a1]

In[10]:= MemoryInUse[]

Out[10]= 41259120
POSTED BY: Frank Kampas

This is indeed a lot faster; how about the memory consumption? The {331776, 4, 4} - array should take up some memory...
POSTED BY: Sander Huisman

I've come up with a faster way to generate all the 4x4 arrays with different numbers in each row and column. See In[3]

In[1]:= Timing @ Dimensions[p4 = Permutations[Range[4]]]

Out[1]= {0., {24, 4}}

In[2]:= Timing @ Dimensions[a1 = Tuples[p4, 4]] 

Out[2]= {0.015625, {331776, 4, 4}}

In[3]:= Timing @ Dimensions[a2 = Intersection[a1, Transpose /@ a1]]

Out[3]= {0.09375, {576, 4, 4}}

In[4]:= Timing @ 
 Dimensions[a3 = Select[a2, #[[1, 1]]*#[[1, 2]]*#[[2, 2]] == 12 &]]

Out[4]= {0., {112, 4, 4}}

In[5]:= Timing @ 
 Dimensions[a4 = Select[a3, Abs[Log[#[[1, 3]]/#[[1, 4]]]] == Log[2] &]]

Out[5]= {0., {64, 4, 4}}

In[6]:= Timing @ 
 Dimensions[
  a5 = Select[
    a4, #[[2, 1]] + #[[3, 1]] + #[[3, 2]] + #[[4, 1]] == 11 &]]

Out[6]= {0., {8, 4, 4}}

In[7]:= Timing @ 
 Dimensions[a6 = Select[a5, Abs[#[[2, 3]] - #[[3, 3]]] == 2 &]]

Out[7]= {0., {6, 4, 4}}

In[8]:= Timing @ Dimensions[a7 = Select[a6, #[[2, 4]] == 2 &]]

Out[8]= {0., {1, 4, 4}}

In[9]:= a7[[1]]

Out[9]= {{1, 3, 2, 4}, {3, 4, 1, 2}, {4, 2, 3, 1}, {2, 1, 4, 3}}
POSTED BY: Frank Kampas

Thanks Frank! BTW: You can see the `intermediate' steps by changing the code a little:

n = 4;
hints = {
   {12, Times, {{1, 1}, {2, 1}, {2, 2}}},
   {2, Divide, {{3, 1}, {4, 1}}},
   {11, Plus, {{1, 2}, {1, 3}, {1, 4}, {2, 3}}},
   {2, Minus, {{3, 2}, {3, 3}}},
   {2, Plus, {{4, 2}}},
   {4, Plus, {{4, 3}, {4, 4}}},
   {3, Minus, {{2, 4}, {3, 4}}}
   };
AbsoluteTiming[
 cands = ConstantArray[Range[n], {n, n}];
 old = False;
 While[old =!= cands,
  Print[DrawGrid[cands, hints]];
  old = cands;
  AbsoluteTiming[ApplyHint @@@ hints;];
  NakedSubset /@ Range[Ceiling[n/2]];
  ];
 ]

Enjoy!
POSTED BY: Sander Huisman

Hidden Subsets can also be implemented by just looking for naked subsets larger than n/2. Change the line:

  NakedSubset /@ Range[Ceiling[n/2]];

to:

  NakedSubset /@ Range[n];

in order to 'implement' 'hidden subsets' (we are looking for large naked subsets, which is equivalent, might be slower though...).
POSTED BY: Sander Huisman

Your method is an impressive implementation in Mathematica of how KenKen is done "by hand".
POSTED BY: Frank Kampas

Note that this solution works in a totally different way than the original. While the original creates all the possible solutions for the entire grid, and filter by crossing out solutions for the entire grid, this implementation find all the possible candidates for each cells. And filters the candidates for each cell until only 1 candidate is left for each cell. Also note that this implementation is much more memory efficient.

Enjoy!
POSTED BY: Sander Huisman

I made a little solver that seems to work (tested 2 different grids), but might not solve all grids. Here is the code:

hintstyle = Sequence[11, Red];
candstyle = Sequence[8, Gray];
fixedstyle = Sequence[22];
opchars = {Plus -> "+", Minus -> "-", Times -> "\[Times]", 
   Divide -> "\[Divide]"};

ClearAll[SquareSides, ClueText, DrawGrid]
SquareSides[n_, m_] := Module[{},
  {{{n, -m}, {n + 1, -m}},
   {{n, -m}, {n, -m - 1}},
   {{n + 1, -m}, {n + 1, -m - 1}},
   {{n, -m - 1}, {n + 1, -m - 1}}
   }
  ]
ClueText[cands_, {x_, y_}] := Module[{center, r = 0.2, cp},
  center = {x + 0.5, -y - 0.5};
  If[Length[cands] == 1,
   Text[Style[First[cands], fixedstyle], center]
   ,
   cp = CirclePoints[center, {r, \[Pi]/2}, n];
   cp = MapThread[
      Text[Style[#1, candstyle], #2] &, {Range[n], cp}][[cands]];
   cp
   ]
  ]
DrawGrid[cands_List, hints_List] := 
 Module[{hor, ver, all, rem, boxborders, topleft, hinttext, candpos, 
   candtext},
  hor = Flatten[Outer[List, Range[n], Range[n + 1]], 1];
  ver = Flatten[Outer[List, Range[n + 1], Range[n]], 1];
  all = Join[{#, # + {1, 0}} & /@ hor, {#, # + {0, 1}} & /@ ver];
  all[[All, All, 2]] *= -1;
  topleft = First[TakeSmallestBy[#, Total, 1]] & /@ hints[[All, 3]];
  topleft += 0.08;
  topleft[[All, 2]] *= -1;
  hinttext = ToString[#1] <> (#2 /. opchars) & @@@ hints;
  hinttext = 
   MapThread[
    Text[Style[#1, hintstyle], #2, {-1, 1}] &, {hinttext, topleft}];
  boxborders = Apply[SquareSides, hints[[All, 3]], {2}];
  boxborders = Flatten[#, 1] & /@ boxborders;
  boxborders = 
   Select[Tally[#], Last[#] == 1 &][[All, 1]] & /@ boxborders;
  boxborders = Flatten[boxborders, 1];
  rem = Complement[all, boxborders];
  candpos = Tuples[Range[n], 2];
  candtext = MapThread[ClueText, {Flatten[cands, 1], candpos}];
  Graphics[{{Gray, Thickness[0.005], Line /@ rem},
    hinttext,
    {Thickness[0.01], Line[boxborders]},
    candtext
    }, ImageSize -> 65 n]
  ]

ClearAll[ApplyHint, DivideFunc, MinusFunc]
DivideFunc[x_, y_] := Abs[Log[x/y]]
MinusFunc[x_, y_] := Abs[x - y]
ApplyHint[ans_Integer, op : Divide | Minus, cells_List] := 
 Module[{cns},
  If[Length[cells] == 2,
   Switch[op,
    Divide, ApplyHint[Log[ans], DivideFunc, cells],
    Minus, ApplyHint[ans, MinusFunc, cells]
    ]
   ,
   Print["Divide/Minus should have 2 cells!!"];
   Abort[];
   ]
  ]
ApplyHint[ans_, op : (Times | Plus | DivideFunc | MinusFunc), 
  cells_List] := Module[{cns},
  cns = Extract[cands, cells];
  cns = Select[Tuples[cns], op @@ # == ans &];
  (* TODO: not only should the 'ans' match, 
  but also we can not have the same values in the same row/column, 
  filter for that here\[Ellipsis] *)

  cns = DeleteDuplicates /@ (cns\[Transpose]);
  MapThread[(Part[cands, Sequence @@ #2] = #1) &, {cns, cells}]
  ]

ClearAll[DeleteCands]
DeleteCands[{n_, m_}, 
  del_] := (Part[cands, n, m] = Complement[Part[cands, n, m], del])

ClearAll[NakedSubset, SameValsCorrectnQ, NakedDelete]
SameValsCorrectnQ[cells_, n_Integer] := Module[{celldata},
  celldata = Extract[cands, cells];
  If[AllTrue[celldata, Length[#] == n &],
   Equal @@ (Sort /@ celldata)
   ,
   False
   ]
  ]
NakedSubset[m_Integer] := Module[{cellgroups},
  cellgroups = 
   Join[Outer[List, Range[n], Range[n]], 
    Outer[List, Range[n], Range[n]]\[Transpose]];
  Do[NakedSubset[m, cg], {cg, cellgroups}]
  ]
NakedSubset[m_Integer, cells_List] := Module[{subsets},
  subsets = Subsets[cells, {m}];
  subsets = Select[subsets, SameValsCorrectnQ[#, m] &];
  Do[NakedDelete[cells, ss], {ss, subsets}]
  ]
NakedDelete[cells_List, samesubs_List] := Module[{other, digits},
  other = Complement[cells, samesubs];
  digits = First[Extract[cands, samesubs[[{1}]]]];
  Do[DeleteCands[o, digits], {o, other}]
  ]

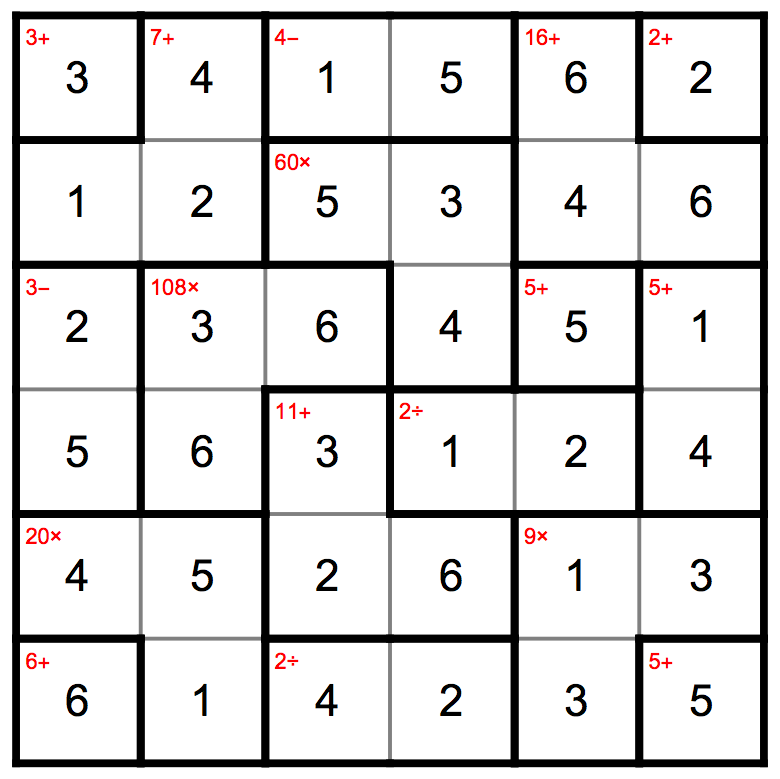
A puzzle has a size and some hints, and then we solve it:

n = 6;
hints = {
   {3, Plus, {{1, 1}}},
   {7, Plus, {{2, 1}, {1, 2}, {2, 2}}},
   {4, Minus, {{3, 1}, {4, 1}}},
   {16, Plus, {{5, 1}, {5, 2}, {6, 2}}},
   {2, Plus, {{6, 1}}},
   {60, Times, {{3, 2}, {4, 2}, {4, 3}}},
   {3, Minus, {{1, 3}, {1, 4}}},
   {108, Times, {{3, 3}, {2, 3}, {2, 4}}},
   {5, Plus, {{5, 3}}},
   {5, Plus, {{6, 3}, {6, 4}}},
   {11, Plus, {{3, 4}, {3, 5}, {4, 5}}},
   {2, Divide, {{4, 4}, {5, 4}}},
   {20, Times, {{1, 5}, {2, 5}, {2, 6}}},
   {9, Times, {{5, 5}, {5, 6}, {6, 5}}},
   {6, Plus, {{1, 6}}},
   {2, Divide, {{3, 6}, {4, 6}}},
   {5, Plus, {{6, 6}}}
   };

AbsoluteTiming[
 cands = ConstantArray[Range[n], {n, n}];
 old = False;
 While[old =!= cands,
  old = cands;
  AbsoluteTiming[ApplyHint @@@ hints;];
  NakedSubset /@ Range[Ceiling[n/2]];
  ];
 ]
DrawGrid[cands, hints]

Giving:

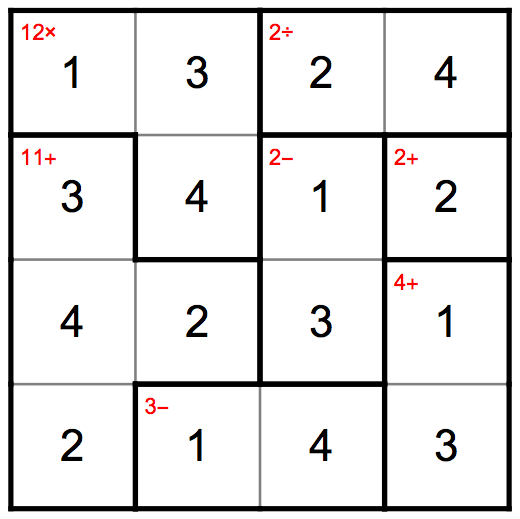
enter image description here

Or for the original problems:

n = 4;
hints = {
   {12, Times, {{1, 1}, {2, 1}, {2, 2}}},
   {2, Divide, {{3, 1}, {4, 1}}},
   {11, Plus, {{1, 2}, {1, 3}, {1, 4}, {2, 3}}},
   {2, Minus, {{3, 2}, {3, 3}}},
   {2, Plus, {{4, 2}}},
   {4, Plus, {{4, 3}, {4, 4}}},
   {3, Minus, {{2, 4}, {3, 4}}}
   };
AbsoluteTiming[
 cands = ConstantArray[Range[n], {n, n}];
 old = False;
 While[old =!= cands,
  old = cands;
  AbsoluteTiming[ApplyHint @@@ hints;];
  NakedSubset /@ Range[Ceiling[n/2]];
  ];
 ]
DrawGrid[cands, hints]

Giving:

enter image description here

Solves it within 10 milliseconds for me. It by no means solves all the KenKen puzzles, once should add the Hidden Subsets technique and eliminate possibilities that I commented in the code.

Cheers!
POSTED BY: Sander Huisman

Updated code:

In[11]:= Timing @ Dimensions[p4 = Permutations[Range[4]]]

Out[11]= {0., {24, 4}}

In[12]:= Timing @ Dimensions[a1 = Tuples[p4, 4]] 

Out[12]= {0., {331776, 4, 4}}

In[13]:= Timing @ 
 Dimensions[a2 = Select[a1, Total[#] == {10, 10, 10, 10} &]]

Out[13]= {0.578125, {2520, 4, 4}}

In[14]:= Timing @ 
 Dimensions[
  a3 = Select[a2, 
    And @@ (And @@ ( Unequal @@ #) &) /@ Transpose[#] &]] 

Out[14]= {0.015625, {576, 4, 4}}

In[15]:= Timing @ 
 Dimensions[a4 = Select[a3, #[[1, 1]]*#[[1, 2]]*#[[2, 2]] == 12 &]]

Out[15]= {0., {112, 4, 4}}

In[16]:= Timing @ 
 Dimensions[a5 = Select[a4, Abs[Log[#[[1, 3]]/#[[1, 4]]]] == Log[2] &]]

Out[16]= {0., {64, 4, 4}}

In[17]:= Timing @ 
 Dimensions[
  a6 = Select[
    a5, #[[2, 1]] + #[[3, 1]] + #[[3, 2]] + #[[4, 1]] == 11 &]]

Out[17]= {0., {8, 4, 4}}

In[18]:= Timing @ 
 Dimensions[a7 = Select[a6, Abs[#[[2, 3]] - #[[3, 3]]] == 2 &]]

Out[18]= {0., {6, 4, 4}}

In[19]:= Timing @ Dimensions[a8 = Select[a7, #[[2, 4]] == 2 &]]

Out[19]= {0., {1, 4, 4}}

In[20]:= a8[[1]]

Out[20]= {{1, 3, 2, 4}, {3, 4, 1, 2}, {4, 2, 3, 1}, {2, 1, 4, 3}}
POSTED BY: Frank Kampas

Can the puzzle itself be automatically and randomly generated ? Then a generated puzzle and its solution would make a complete application like an app at Demonstration Project.

POSTED BY: Sam Carrettie

I've done Sudoku, doing it one row at a time, rather than generating all possible grids at the start.
I think that approach would also work for larger KenKen.

http://library.wolfram.com/infocenter/MathSource/7784/
POSTED BY: Frank Kampas

O btw, you can simply one of your filters:

Unequal[Sequence @@ #]

can be

Unequal @@ #

Very nice idea though, but I don't think this will work for a 6*6 grid or even larger...
POSTED BY: Sander Huisman

Alternatively, one can reorder your 'filters':

a1 = Select[a1, #[[2, 4]] == 2 &];
a1 = Select[a1, #[[1, 1]]*#[[1, 2]]*#[[2, 2]] == 12 &];
a1 = Select[a1, Abs[#[[2, 3]] - #[[3, 3]]] == 2 &];
a1 = Select[a1, #[[2, 1]] + #[[3, 1]] + #[[3, 2]] + #[[4, 1]] == 11 &];
a1 = Select[a1, (And @@ (And @@ Unequal[Sequence @@ #] &) /@ Transpose[#]) &];
a1 = Select[a1, Abs[Log[#[[1, 3]]/#[[1, 4]]]] == Log[2] &];

They 6 filters reduce all the sets to the right one. The order can be changed resulting in the same answer. I tried all possible permutations of these 6 filters, the above one is the fastest order. (around 0.80 seconds on my computer, while the order given by Frank gives me over 5 seconds.)
POSTED BY: Sander Huisman

Very interesting, it's like sudoku, but a little bit more sophisticated. I added an extra step to your code which speeds it up 5X.

start=AbsoluteTime[];
Dimensions[p4=Permutations[Range[4]]]
Dimensions[a1=Flatten[Outer[List,p4,p4,p4,p4,1],3]]
Dimensions[a1=Select[a1,Total[#]=={10,10,10,10}&]]
Dimensions[a2=Select[a1,(And@@(And@@Unequal[Sequence@@#]&)/@Transpose[#])&]]
Dimensions[a3=Select[a2,#[[1,1]]*#[[1,2]]*#[[2,2]]==12&]]
Dimensions[a4=Select[a3,Abs[Log[#[[1,3]]/#[[1,4]]]]==Log[2]&]]
Dimensions[a5=Select[a4,#[[2,1]]+#[[3,1]]+#[[3,2]]+#[[4,1]]==11&]]
Dimensions[a6=Select[a5,Abs[#[[2,3]]-#[[3,3]]]==2&]]
Dimensions[a7=Select[a6,#[[2,4]]==2&]]
a7
AbsoluteTime[]-start

Note that I overwrite a1 on line 4. This substantially reduces the number of grids and the operation is very fast.

POSTED BY: Sander Huisman

enter image description here
POSTED BY: Frank Kampas

Very cool, Frank. Is there a link or an image of what you are solving?

POSTED BY: Sam Carrettie
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract