Jim, Good question! I don't know the details of how the data was obtained, but you get a Sinc function if you Fourier transform a rectangle: rectangle function. However if the rectangle is somehow modified by some smoothing function, the resulting transform has a main lobe that is typically wider but has smaller side lobes. Also as this seems to be a measurement, you have background noise that can drown out the lower lobes, which is defined by the signal to noise ratio.

I agree, from the first post I too thought we are dealing with something like a Gaussian distribution, but obviously from the type of measurement a Sinc function is expected.

Hi, This is how I would solve it:

In[270]:= Clear["Global`*"]

In[271]:= 
data = {{27, 2.2}, {27.2, 2.2}, {27.4, 2.3}, {27.6, 2.3}, {27.8, 
    2.2}, {28, 2.2}, {28.2, 2.3}, {28.4, 2.2}, {28.6, 2.2}, {28.8, 
    2.3}, {29, 2.2}, {29.2, 2.2}, {29.4, 2.3}, {29.6, 2.2}, {29.8, 
    2.3}, {30, 2.3}, {30.2, 2.3}, {30.4, 2.3}, {30.6, 2.3}, {30.8, 
    2.3}, {31, 2.3}, {31.2, 2.3}, {31.4, 2.3}, {31.6, 2.3}, {31.8, 
    2.3}, {32, 2.3}, {32.2, 2.3}, {32.4, 2.3}, {32.6, 2.3}, {32.8, 
    2.4}, {33, 2.4}, {33.2, 2.4}, {33.4, 2.4}, {33.6, 2.5}, {33.8, 
    2.6}, {34, 2.7}, {34.2, 2.7}, {34.4, 2.8}, {34.6, 3.5}, {34.8, 
    5.1}, {35, 10.3}, {35.2, 15.4}, {35.4, 21.1}, {35.6, 29.1}, {35.8,
     35.6}, {36, 38.4}, {36.2, 37.5}, {36.4, 32.8}, {36.6, 
    25.5}, {36.8, 17.5}, {37, 10.9}, {37.2, 6.4}, {37.4, 3.8}, {37.6, 
    2.8}, {37.8, 2.7}, {38, 2.9}, {38.2, 2.8}, {38.4, 2.7}, {38.6, 
    2.4}, {38.8, 2.3}, {39, 2.3}, {39.2, 2.4}, {39.4, 2.4}, {39.6, 
    2.4}, {39.8, 2.4}, {40, 2.3}};

In[272]:= \
(*pd=ListLogPlot[data,PlotStyle\[Rule]Red,PlotTheme\[Rule]"Detailed"]*)

In[273]:= nlm = 
 FindFit[data, pp (Sinc[a x - tt])^2 + q, {a, pp, tt, q, m}, x, 
  Method -> NMinimize]

Out[273]= {a -> -1.9653, pp -> 35.9368, tt -> -70.833, q -> 2.05044, 
 m -> -35.6927}

In[274]:= fitx[x_] = pp (Sinc[a x - tt])^2 + q /. %

Out[274]= 2.05044 + 35.9368 Sinc[70.833 - 1.9653 x]^2

In[275]:= (*fitp=LogPlot[fitx[x],{x,27,40},PlotStyle\[Rule]Green]*)

In[276]:= (*Show[pd,fitp]*)

I modified your equation took out the "m x" term and I used Sinc^2 instead Sin^2/x (not the same as Sin^2/x^2) not sure if you wanted that. "Method -> NMinimize" does the trick for this kind of fit. this is what I get:

NonlinearModelFit is probably working just fine. It's your model using a sine wave that's the problem. While the points show a definite peak that isn't the shape of a sine wave (which has a peak and a trough and repeats) although if you restricted your fit of a sine to about 35 to 37, you might do better.

If you're mainly interested in approximating the curve (in Mathematica and not outside of Mathematica), then I recommend using the Interpolation function:

data = {{27, 2.2}, {27.2, 2.2}, {27.4, 2.3}, {27.6, 2.3}, {27.8, 2.2}, {28, 2.2}, {28.2, 2.3}, {28.4, 2.2}, {28.6, 2.2},
   {28.8, 2.3}, {29, 2.2}, {29.2, 2.2}, {29.4, 2.3}, {29.6, 2.2}, {29.8, 2.3}, {30, 2.3}, {30.2, 2.3}, {30.4, 2.3}, 
   {30.6, 2.3}, {30.8, 2.3}, {31, 2.3}, {31.2, 2.3}, {31.4, 2.3}, {31.6, 2.3}, {31.8, 2.3}, {32, 2.3}, {32.2, 2.3}, {32.4, 2.3},
   {32.6, 2.3}, {32.8, 2.4}, {33, 2.4}, {33.2, 2.4}, {33.4, 2.4}, {33.6, 2.5}, {33.8, 2.6}, {34, 2.7}, {34.2, 2.7}, {34.4, 2.8},
   {34.6, 3.5}, {34.8, 5.1}, {35, 10.3}, {35.2, 15.4}, {35.4, 21.1}, {35.6, 29.1}, {35.8, 35.6}, {36, 38.4}, {36.2, 37.5},
   {36.4, 32.8}, {36.6, 25.5}, {36.8, 17.5}, {37, 10.9}, {37.2, 6.4}, {37.4, 3.8}, {37.6, 2.8}, {37.8, 2.7}, {38, 2.9}, 
   {38.2, 2.8}, {38.4, 2.7}, {38.6, 2.4}, {38.8, 2.3}, {39, 2.3}, {39.2, 2.4}, {39.4, 2.4}, {39.6, 2.4}, {39.8, 2.4}, {40, 2.3}};
f = Interpolation[data];
Plot[f[x], {x, 27, 40}, PlotStyle -> Red, PlotRange -> Full];pPoints = ListPlot[data, PlotRange -> Full, PlotStyle -> Blue];
Show[{pInterpolation, pPoints}]

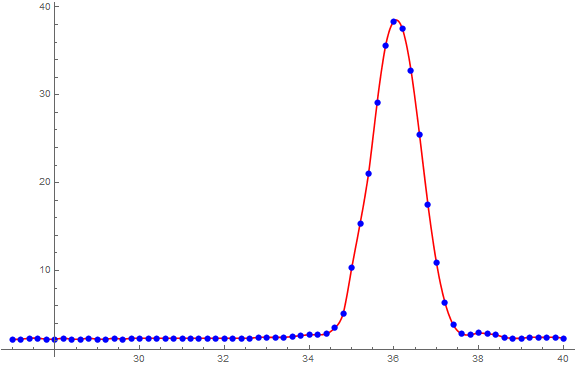
But if you need a curve form with parameters to estimate so that you can use the predictions outside of Mathematica (and for which you can decide visually if the fit is good enough), then you might want to try something like

pNormalCurve = 
  Plot[2.1 + 55 PDF[NormalDistribution[36.05, 0.6], x], {x, 27, 40}, 
   PlotRange -> Full, PlotStyle -> {Thickness[0.02], LightGray}];
Show[{pNormalCurve, pInterpolation, pPoints}, ImageSize -> Large]

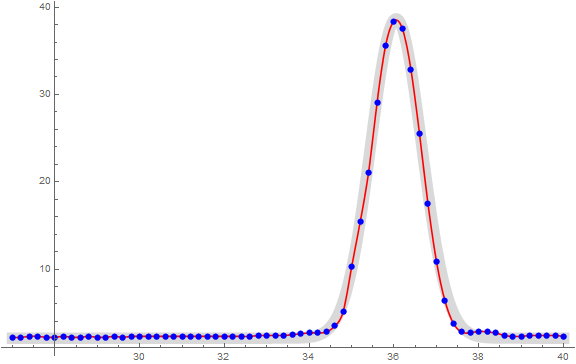
where the thick gray line is the normal curve fit. (I just did this by eye but you can use NonlinearModelFit also.)

If you need so say something about the parameters (i.e., measures of precision) and/or prediction errors, then something appropriate (in my opinion) depends on how the data is generated, if there will be multiple data sets which a need to compare parameters, how the residuals look, etc.