Joerg, thank you for posting this. Though it is a neat pattern-based approach, I should notice that finding all maxima can be done with built in function MaxDetect. I was looking for something else - resolving in time two highest strange peaks - basically putting time stamp on them so we could start searching for a reasonable explanations of why did they happen. Now, having been armed with
community-derived function for finding peaks, we can finally found out when did the spikes happen. Just in case, I repeat here the definition of the function:
FindPeaks =
Compile[{{data, _Real,
1}, {width, _Integer}, {cut, _Real}}, (Table[0, {width}]~Join~
UnitStep[
Take[data, {1 + width, -1 -
width}] - (Module[{tot = Total[#1[[1 ;; #2 - 1]]],
last = 0.}, Table[tot = tot + #1[[j + #2]] - last;
last = #1[[j + 1]];
tot, {j, 0, Length[#1] - #2}]]/#2) &[data,
1 + 2 width] - cut]~Join~Table[0, {width}]) ({0}~Join~
Table[If[
Sign[{data[[ii + 1]] - data[[ii]],
data[[ii + 2]] - data[[ii + 1]]}] == {1, -1}, 1, 0], {ii,
1, Length[data] - 2}]~Join~{0}), CompilationTarget -> "C"];
Now let's get the data:
raw = WolframAlpha["Aristotle", {{"PopularityPod:WikipediaStatsData", 1}, "TimeSeriesData"}];
data = raw[[All, 2]][[All, 1]];
and with a bit convoluted code I will place time stamps on strange peaks:
Show[DateListPlot[raw, Joined -> True, AspectRatio -> 1/6, ImageSize -> 800, Filling -> Bottom,
Ticks -> {{#, Rotate[DateString[#, {"MonthNameShort", " ", "Year"}], Pi/2]} & /@ #[[All, 1]], Automatic},
Frame -> False, Mesh -> All, PlotRange -> All], DateListPlot[If[# == {}, raw[[1 ;; 2]], #, #] &[#],
AspectRatio -> 1/6, ImageSize -> 800, PlotStyle -> Directive[Red, PointSize[.007]], PlotRange -> All],
PlotRangePadding -> {0, Automatic}] &[Pick[raw, FindPeaks[data, 1, 2 StandardDeviation[data]], 1]]
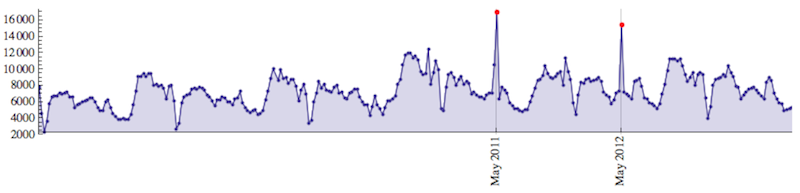
And voila! - they both land on May . Maybe in some schools students got an assignment to write a term paper on Aristotle or maybe a textbook was published with some homework on Aristotle. All that could be required to be hand in at the end of semester. Or anything similar. The most suspicious thing is why didn't it happen in previous or the next 2013 year? Well a lot of ground for speculations.
What are your thoughts? What could be a possible root to solving this mystery?