It is best to give your variables some plain understandable names. Like in you function:( this is a spring with diameter and start and endpoint)
springmass[start_: 0, end_, diameter_] :=
Module[{a = diameter, y1 = start, y2 = end, n = 100}, h = (y2 - y1)/n;
yvalues = Table[k, {k, y1, y2, h}];
xvalues = Table[a Sin[(m \[Pi])/2], {m, 0, n}];
Line[Transpose[{xvalues, yvalues}]]]
This will then make a simple manipulate:
Manipulate[With[{size = .2},
Animate[
Graphics[{
vspring[diameter, start, 2 Sin[y]],
Red, Thickness[5 size],
Line[{{-.5 size, 2 Sin[y]}, {.5 size, 2 Sin[y]}}]},
PlotRange -> {{-size, size}, {-2.2, 2 size}}, Axes -> True,
ImageSize -> Small],
{y, -\[Pi], 0, 0.1}]],
{{diameter, .2}, .05, 1},
{{start, 0}, -1, 1}]
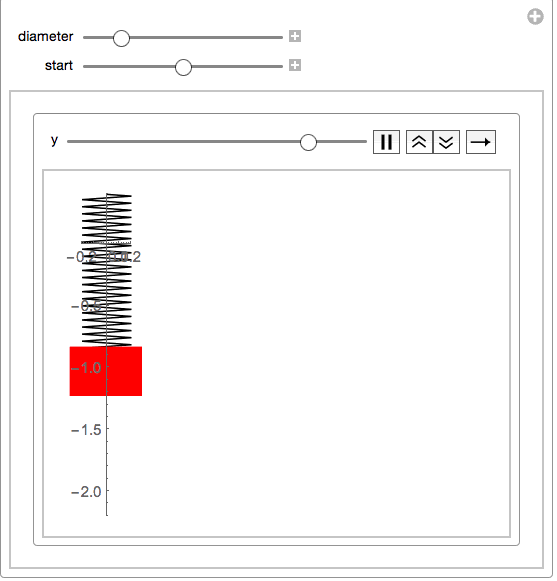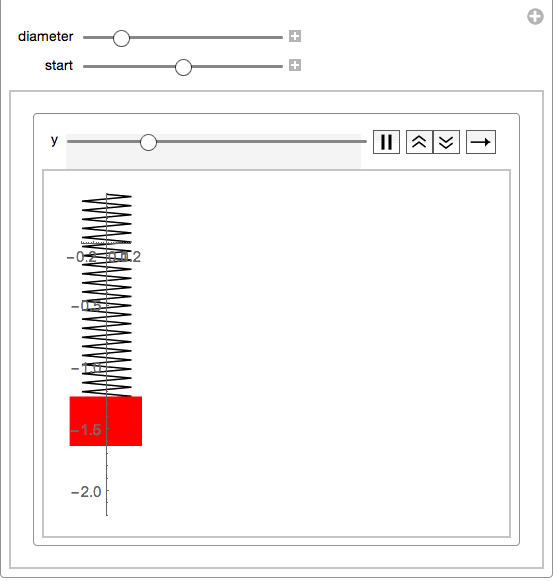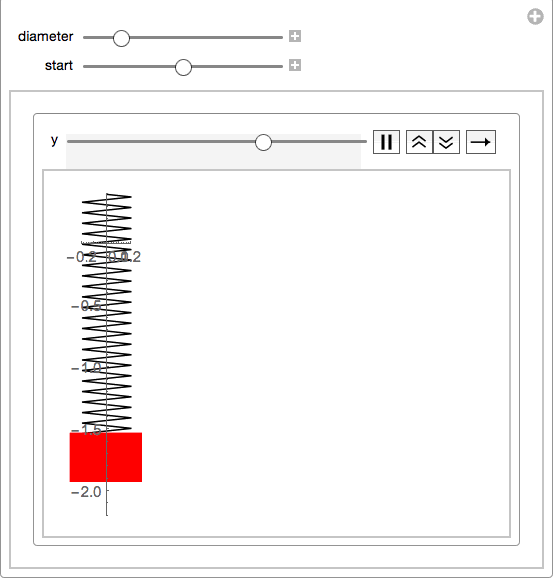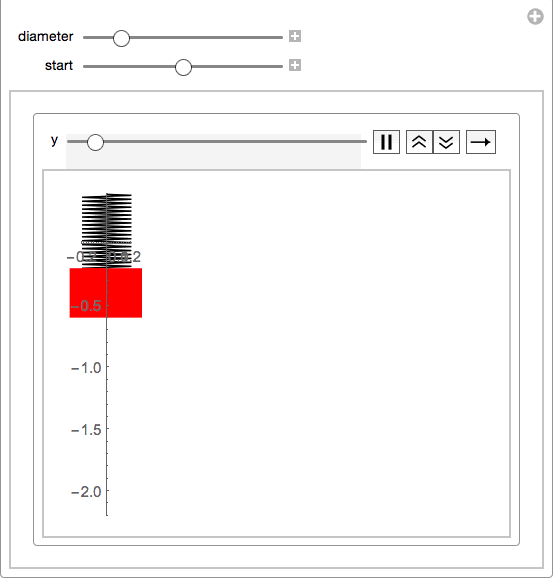
your function springs eliminates the strapping and considers it to be zero:springmass[start: 0, end, diameter_] :=
Module[{a = diameter, y1 = start, y2 = end, n = 100}, h = (y2 - y1)/n;
yvalues = Table[k, {k, y1, y2, h}];
xvalues = Table[a Sin[(m [Pi])/2], {m, 0, n}];
Line[Transpose[{xvalues, yvalues}]]]
This way no need for a third variable since the default value _:0 will be chosen.
Animate[Graphics[springmass[5 + Sin[\[CurlyPhi]], 1],
PlotRange -> {{-5, 5}, {0, 7}}, Axes -> True], {\[CurlyPhi], 0,
2 \[Pi]}]
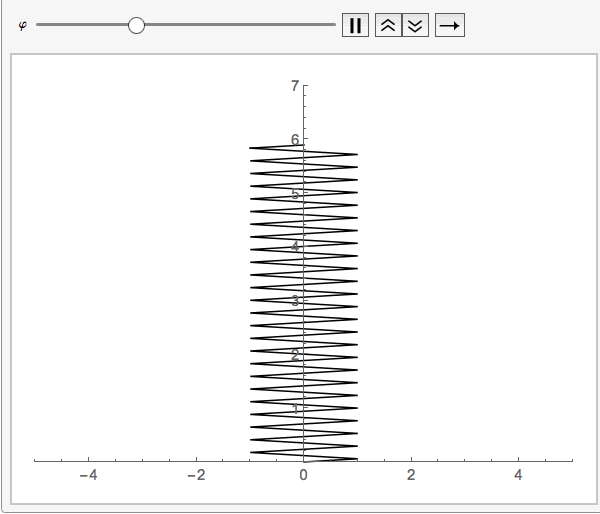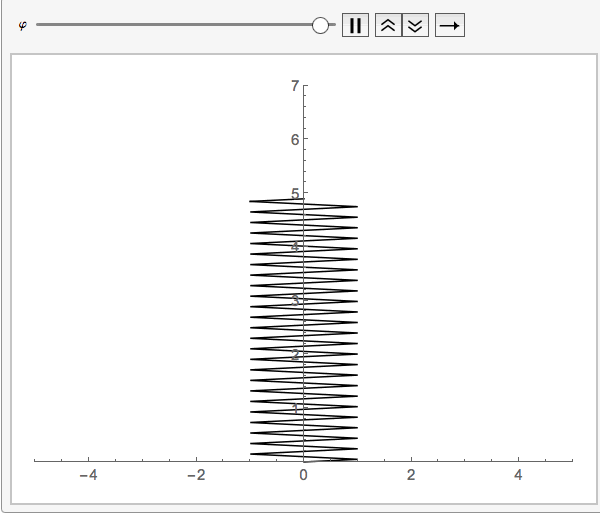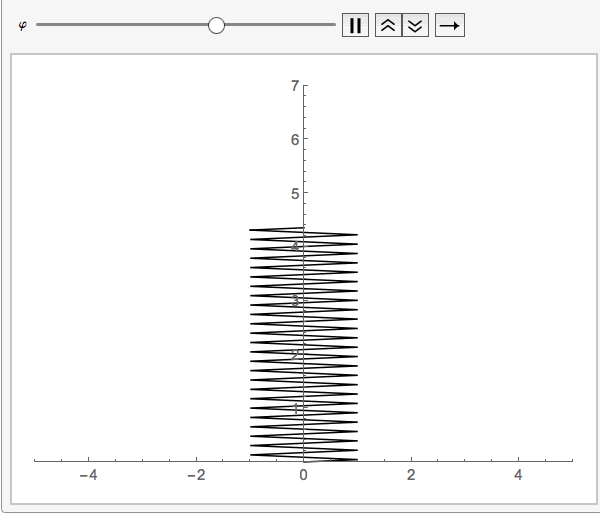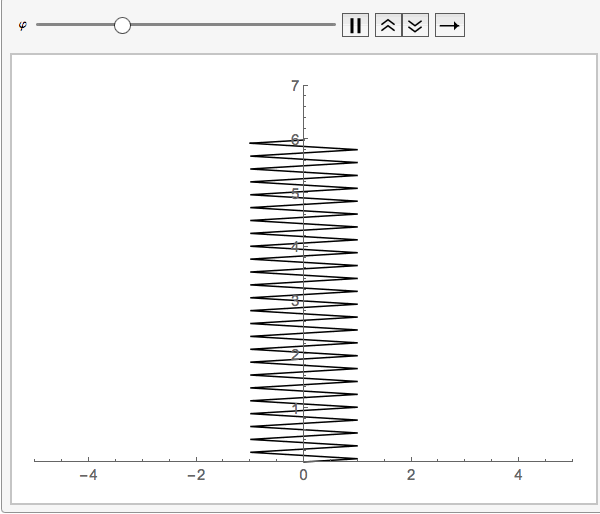
It is better to explain the question more in detail since it was hard to guess what this was all about. But this will hopefully be of help.