Since there is a parameter (It is not very clear what this parameter is but, I presume, like David, it is the initial condition y[x,0] (let it be alpha):
In this case, ParametricNDSolve is a good choice
In[236]:= Clear[\[Alpha], sol, y]
a = 100; T = 60000; L = \[Pi];
sol = ParametricNDSolve[{I \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(y[x, t]\)\) + .0004 \!\(
\*SubscriptBox[\(\[PartialD]\), \(x, x\)]\(y[x, t]\)\) == 0,
y[-a, t] == y[a, t],
y[x, 0] ==
Piecewise[{{0, x < -(L/2)}, {0,
x > L/2}, {Sqrt[2/L] \[Alpha] Cos[x], -(L/2) <= x <= L/2}}]},
y, {x, -a, a}, {t, 0, T}, {\[Alpha]}];
y /. sol
y[.1] /. sol
%[0., 0.5]
Out[239]= ParametricFunction[ <> ]
Out[240]= InterpolatingFunction[{{\[Ellipsis], -100.,
100., \[Ellipsis]}, {0., 60000.}}, <>]
Out[241]= 0.0797883 - 5.73532*10^-7 I
and the Plot3D is really affected by the value of alpha as can be seen with a Manipulate:
Manipulate[
Quiet@Plot3D[
Evaluate[Abs[y[\[Alpha]][x, t]] /. sol], {x, -100, 100}, {t, -3.5,
3.5},
PlotRange -> All, PlotPoints -> 50], {{\[Alpha], 1.57}, -5,
10, .01, Appearance -> "Labeled"}, SynchronousUpdating -> False]
![][1]
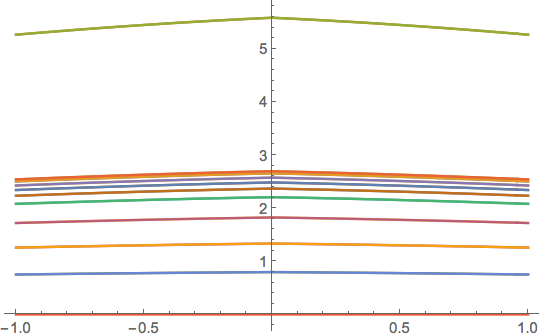
The effect of alpha can also be seen from the following plot:
Plot[Evaluate[
Table[Abs[y[\[Alpha]][x, .95] /. sol], {\[Alpha], -10,
10}]], {x, -1, 1}]