At MathWorld, there's the Heawood graph. Noted there and over at Wikipedia there are some unit distance embeddings, where all edges have length 1. But none has symmetry. Let's fix that.
pts=N[{ {-1/2,-(1/2) (-1+Sqrt[3-4 x-4 x^2])}, {x,1/2}, {x,-1/2}, {-1/2,1/2 (-1+Sqrt[3-4 x-4 x^2])}, {1/2,1/2 (-1+Sqrt[3-4 x-4 x^2])}, {-x,-1/2}, {-x,1/2}, {1/2,-(1/2) (-1+Sqrt[3-4 x-4 x^2])}, {1/2 (-1+Sqrt[3-4 x (1+x)]) Sqrt[(7+8 Sqrt[3-4 x (1+x)]-8 x (-1+x (1+2 x (2+x))))/(13+8 x (1+x) (-3+2 x (1+x)))],-(1/2) Sqrt[(7+8 Sqrt[3-4 x (1+x)]-8 x (-1+x (1+2 x (2+x))))/(13+8 x (1+x) (-3+2 x (1+x)))]},{Sqrt[3-4 x^2]/(2 Sqrt[1+4 x^2]),-((x Sqrt[3-4 x^2])/Sqrt[1+4 x^2])}, {-Sqrt[3-4 x^2]/(2 Sqrt[1+4 x^2]),-((x Sqrt[3-4 x^2])/Sqrt[1+4 x^2])}, {-(1/2) (-1+Sqrt[3-4 x (1+x)]) Sqrt[(7+8 Sqrt[3-4 x (1+x)]-8 x (-1+x (1+2 x (2+x))))/(13+8 x (1+x) (-3+2 x (1+x)))],-(1/2) Sqrt[(7+8 Sqrt[3-4 x (1+x)]-8 x (-1+x (1+2 x (2+x))))/(13+8 x (1+x) (-3+2 x (1+x)))]} , {1/2,-((x Sqrt[3-4 x^2])/Sqrt[1+4 x^2])-Sqrt[(8 x^2+Sqrt[3+8 x^2-16 x^4])/(2+8 x^2)]}, {-1/2,-((x Sqrt[3-4 x^2])/Sqrt[1+4 x^2])-Sqrt[(8 x^2+Sqrt[3+8 x^2-16 x^4])/(2+8 x^2)]} }/.x->Root[-153027+1353114 #1-1986024 #1^2+2763312 #1^3+10497808 #1^4+31063072 #1^5-8457728 #1^6-40590336 #1^7+44468736 #1^8+164975616 #1^9+119705600 #1^10-494067712 #1^11-763912192 #1^12+414924800 #1^13+1154613248 #1^14+48496640 #1^15-864485376 #1^16-376307712 #1^17+253231104 #1^18+271581184 #1^19+89128960 #1^20+10485760 #1^21&,1],300];
points = pts[[#]] & /@ {13, 12, 4, 5, 9, 14, 11, 3, 2, 1, 8, 7, 6, 10};
edges = {{1, 2}, {1, 6}, {1, 14}, {2, 3}, {2, 11}, {3, 4}, {3, 8}, {4, 5}, {4,13}, {5, 6}, {5, 10}, {6, 7}, {7, 8}, {7, 12}, {8, 9}, {9, 10}, {9,14}, {10, 11}, {11, 12}, {12, 13}, {13, 14}}
These are the same edges as GraphData["HeawoodGraph", "EdgeIndices"]
Graphics[{Red, Disk[#, .02] & /@ points, Black, Line[{points[[#[[1]]]], points[[#[[2]]]]}] & /@ edges}]
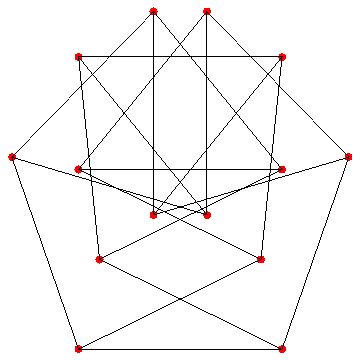
With this code, we can verify that all the edges are 1.
EuclideanDistance[points[[#[[1]]]], points[[#[[2]]]]] & /@ edges
So, how did I find this? I originally had the 8 points at the top in a regular octagon, but that made the bottom edge longer than 1. I needed an 8 cycle where all the edges had length 1.
MyEuc[{a, b}, {c, d}] := Sqrt[(a - c)^2 + (b - d)^2]; Solve[MyEuc[{x, 1/2}, {-1/2, -y}] == 1]
That gives the first eight pts. Next we need pts 9 at a distance of 1 from pts 1 and 5.
{a, b} /. FullSimplify[Solve[{MyEuc[pts[[1]], {a, b}] == 1, MyEuc[pts[[5]], {a, b}] == 1}]]
Turns out we want the second of those. With symmetry, we have pts 1-12. For the last 2,
b /. FullSimplify[Solve[{MyEuc[{Sqrt[3 - 4 x^2]/(2 Sqrt[1 + 4 x^2]), -((x Sqrt[3 - 4 x^2])/Sqrt[1 + 4 x^2])}, {1/2, b}] == 1}]]
From that, we get the last two points.
{1/2, -((x Sqrt[3 - 4 x^2])/Sqrt[1 + 4 x^2]) - Sqrt[(8 x^2 + Sqrt[3 + 8 x^2 - 16 x^4])/(2 + 8 x^2)]}
To solve for x, we need a solution for a nasty equation. Solve[] wasn't working, so I tried a trick.
NMinimize[{Abs[ Sqrt[(((x Sqrt[3 - 4 x^2])/Sqrt[1 + 4 x^2] + Sqrt[(8 x^2 + Sqrt[3 + 8 x^2 - 16 x^4])/(2 + 8 x^2)] - 1/2 Sqrt[(7 + 8 Sqrt[3 - 4 x (1 + x)] - 8 x (-1 + x (1 + 2 x (2 + x))))/(13 + 8 x (1 + x) (-3 + 2 x (1 + x)))])^2 + (-(1/2) - 1/2 (-1 + Sqrt[3 - 4 x (1 + x)]) Sqrt[(7 + 8 Sqrt[3 - 4 x (1 + x)] - 8 x (-1 + x (1 + 2 x (2 + x))))/(13 + 8 x (1 + x) (-3 + 2 x (1 + x)))])^2)] - 1], .1 < x < .3}, x, AccuracyGoal -> 2000, WorkingPrecision -> 4000]
Then I took that and put it into RootApproximant[] -- and got the solution.
Root[-153027 + 1353114 #1 - 1986024 #1^2 + 2763312 #1^3 + 10497808 #1^4 + 31063072 #1^5 - 8457728 #1^6 - 40590336 #1^7 + 44468736 #1^8 + 164975616 #1^9 + 119705600 #1^10 - 494067712 #1^11 - 763912192 #1^12 + 414924800 #1^13 + 1154613248 #1^14 + 48496640 #1^15 - 864485376 #1^16 - 376307712 #1^17 + 253231104 #1^18 + 271581184 #1^19 + 89128960 #1^20 + 10485760 #1^21 &, 1]
And so, we get an exact unit-distance embedding with the Heawood graph, with symmetry.
 Attachments:
Attachments: