Message Boards Message Boards

GROUPS:
Astronomy
Miriam Ahmed

What's wrong with my code? (Modelling planetary motion)

Miriam Ahmed
Posted 8 years ago
6174 Views
|
2 Replies
|
0 Total Likes
|

Differential equations for modelling planetary motion (3 bodies), getting errors saying that it is 'null'- anyone point out where I've gone wrong?

sols = NDSolve[ {x1''[t] == (G m2 (x2 - x1[t]))/((x2 - x1[t])^2 - (y2 - y1)^2)^(3/ 2) + (G m3 (x3 - x1[t]))/((x3 - x1[t])^2 - (y3 - y1)^2)^(3/2), y1''[t] == (G m2 (y2 - y1[t]))/((x2 - x1)^2 - (y2 - y1[t])^2)^(3/ 2) + (G m3 (y3 - y1[t]))/((x3 - x1)^2 - (y3 - y1[t])^2)^(3/2), x2''[t] == (G m1 (x1 - x2[t]))/((x1 - x2[t])^2 - (y1 - y2)^2)^(3/ 2) + (G m3 (x3 - x2[t]))/((x3 - x2[t])^2 - (y3 - y2)^2)^(3/2), y2''[t] == (G m1 (y1 - y2[t]))/((x1 - x2)^2 - (y1 - y2[t])^2)^(3/ 2) + (G m3 (y3 - y2[t]))/((x3 - x2)^2 - (y3 - y2[t])^2)^(3/2), x3''[t] == (G m1 (x1 - x3[t]))/((x1 - x3[t])^2 - (y1 - y3)^2)^(3/ 2) + (G m2 (x2 - x3[t]))/((x2 - x3[t])^2 - (y2 - y3)^2)^(3/2), y3''[t] == (G m1 (y1 - y3[t]))/((x1 - x3)^2 - (y1 - y3[t])^2)^(3/ 2) + (G m2 (y2 - y3[t]))/((x2 - x3)^2 - (y2 - y3[t])^2)^(3/2), x1[0] == d, y1[0] == 0, x1'[0] == -0.8, y1'[0] == v, x2[0] == d, y2[0] == 0, x2'[0] == -0.8, y2'[0] == v, x3[0] == d, y3[0] == 0, x3'[0] == -0.8, y3'[0] == v} /. {G -> 1, m1 -> 1, m2 -> 1, m3 -> 1, d -> 1, v -> 1,}, {x1[t], y[1 t], x2[t], y2[t], x3[t], y3[t]}, {t, 0, 100}];

(if you paste it into mathematica hopefully it'll look nicer), also I'm a sixteen year old girl so please go easy
POSTED BY: Miriam Ahmed
2 Replies
Sort By:

Hi,

the following equations will produce some output. 

sols = NDSolve[{x1''[
       t] == (G m2 (x2[t] - 
            x1[t]))/((x2[t] - x1[t])^2 - (y2[t] - y1[t])^2)^(3/
           2) + (G m3 (x3[t] - 
            x1[t]))/((x3[t] - x1[t])^2 - (y3[t] - y1[t])^2)^(3/2), 
     y1''[t] == (G m2 (y2[t] - 
            y1[t]))/((x2[t] - x1[t])^2 - (y2[t] - y1[t])^2)^(3/
           2) + (G m3 (y3[t] - 
            y1[t]))/((x3[t] - x1[t])^2 - (y3[t] - y1[t])^2)^(3/2), 
     x2''[t] == (G m1 (x1[t] - 
            x2[t]))/((x1[t] - x2[t])^2 - (y1[t] - y2[t])^2)^(3/
           2) + (G m3 (x3[t] - 
            x2[t]))/((x3[t] - x2[t])^2 - (y3[t] - y2[t])^2)^(3/2), 
     y2''[t] == (G m1 (y1[t] - 
            y2[t]))/((x1[t] - x2[t])^2 - (y1[t] - y2[t])^2)^(3/
           2) + (G m3 (y3[t] - 
            y2[t]))/((x3[t] - x2[t])^2 - (y3[t] - y2[t])^2)^(3/2), 
     x3''[t] == (G m1 (x1[t] - 
            x3[t]))/((x1[t] - x3[t])^2 - (y1[t] - y3[t])^2)^(3/
           2) + (G m2 (x2[t] - 
            x3[t]))/((x2[t] - x3[t])^2 - (y2[t] - y3[t])^2)^(3/2), 
     y3''[t] == (G m1 (y1[t] - 
            y3[t]))/((x1[t] - x3[t])^2 - (y1[t] - y3[t])^2)^(3/
           2) + (G m2 (y2[t] - 
            y3[t]))/((x2[t] - x3[t])^2 - (y2[t] - y3[t])^2)^(3/2), 
     x1[0] == d1, y1[0] == 0, x1'[0] == -0.8, y1'[0] == v1, 
     x2[0] == d2, y2[0] == 0, x2'[0] == -0.2, y2'[0] == v2, 
     x3[0] == d3, y3[0] == 0, x3'[0] == -0.1, 
     y3'[0] == v3} /. {G -> 0.1, m1 -> 1, m2 -> 1, m3 -> 1, d1 -> 10, 
     v1 -> 1, d2 -> 20, v2 -> 2, d3 -> 30, v3 -> 1}, {x1[t], y1[ t], 
    x2[t], y2[t], x3[t], y3[t]}, {t, 0, 10}];

You can plot functions like this:

Plot[{x1[t], x2[t]} /. sols, {t, 0, 10}]

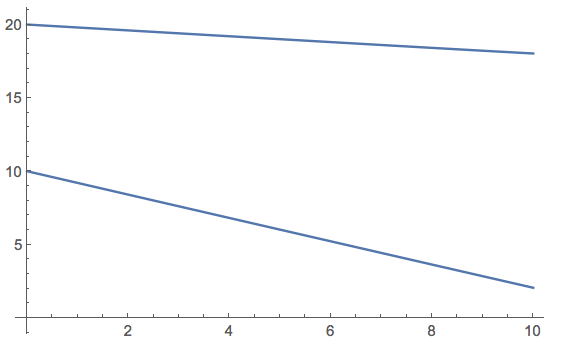
enter image description here

You can also use ParametricPlot:

ParametricPlot[{{x1[t], y1[t]} /. sols, {x2[t], y2[t]} /. sols, {x3[t], y3[t]} /. sols}, {t, 0, 10}, PlotRange -> {{-30, 30}, {-30, 30}}]

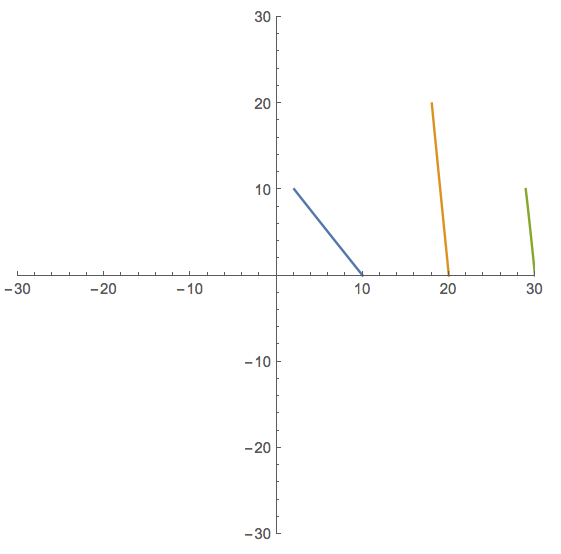
enter image description here

The results are still not what you would expect. This is because your equations for the gravitational force are not correct. Where you divide by the squared distances in the x and y direction you should actually add not subtract:

sols = NDSolve[{x1''[
       t] == (G m2 (x2[t] - 
            x1[t]))/((x2[t] - x1[t])^2 + (y2[t] - y1[t])^2)^(3/
           2) + (G m3 (x3[t] - 
            x1[t]))/((x3[t] - x1[t])^2 + (y3[t] - y1[t])^2)^(3/2), 
     y1''[t] == (G m2 (y2[t] - 
            y1[t]))/((x2[t] - x1[t])^2 + (y2[t] - y1[t])^2)^(3/
           2) + (G m3 (y3[t] - 
            y1[t]))/((x3[t] - x1[t])^2 + (y3[t] - y1[t])^2)^(3/2), 
     x2''[t] == (G m1 (x1[t] - 
            x2[t]))/((x1[t] - x2[t])^2 + (y1[t] - y2[t])^2)^(3/
           2) + (G m3 (x3[t] - 
            x2[t]))/((x3[t] - x2[t])^2 + (y3[t] - y2[t])^2)^(3/2), 
     y2''[t] == (G m1 (y1[t] - 
            y2[t]))/((x1[t] - x2[t])^2 + (y1[t] - y2[t])^2)^(3/
           2) + (G m3 (y3[t] - 
            y2[t]))/((x3[t] - x2[t])^2 + (y3[t] - y2[t])^2)^(3/2), 
     x3''[t] == (G m1 (x1[t] - 
            x3[t]))/((x1[t] - x3[t])^2 + (y1[t] - y3[t])^2)^(3/
           2) + (G m2 (x2[t] - 
            x3[t]))/((x2[t] - x3[t])^2 + (y2[t] - y3[t])^2)^(3/2), 
     y3''[t] == (G m1 (y1[t] - 
            y3[t]))/((x1[t] - x3[t])^2 + (y1[t] - y3[t])^2)^(3/
           2) + (G m2 (y2[t] - 
            y3[t]))/((x2[t] - x3[t])^2 + (y2[t] - y3[t])^2)^(3/2), 
     x1[0] == d1, y1[0] == 0, x1'[0] == -0.8, y1'[0] == v1, 
     x2[0] == d2, y2[0] == 0, x2'[0] == -0.2, y2'[0] == v2, 
     x3[0] == d3, y3[0] == 0, x3'[0] == -0.1, 
     y3'[0] == v3} /. {G -> 2, m1 -> 1, m2 -> 1, m3 -> 1, d1 -> 1, 
     v1 -> 0.1, d2 -> 2, v2 -> 0.2, d3 -> 3, v3 -> 0.4}, {x1[t], 
    y1[ t], x2[t], y2[t], x3[t], y3[t]}, {t, 0, 100}];

You will notice that this is probably still not what you want, or is it?

Cheers,

Marco
POSTED BY: Marco Thiel

Hi Miriam,

it would be helpful tonpost the code in one of the "code-windows". There is a button when you compose your message. Glancing over the code it seems that there are still x and y variables that do not have the time dependence. So x1 should be x1[t].

Cheers,

Marco
POSTED BY: Marco Thiel
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract