We are looking into numerical solution of nonlinear Klein Gordon equation in 3+1 dimensions with periodic boundary conditions. We use a Gaussian as an initial condition. The problem could be solved for a small interval of time t=1. However NDSolve fails and show a ndsz error for higher values of t. We are attaching some plots for the solution we obtained so far.
l=5;k=1;Tf=1;u4[x_,y_,z_,t_]:=Exp[-x^2-y^2-z^2];dim4=NDSolve[{D[u[x,y,z,t],{t,2}]-D[u[x,y,z,t],{x,2}]-D[u[x,y,z,t],{y,2}]+D[u[x,y,z,t],{z,2}]+u[x,y,z,t]-k (u[x,y,z,t])^3==0,u[x,y,z,0]==u4[x,y,z,0],Derivative[0,0,0,1][u][x,y,z,0]==Derivative[0,0,0,1][u4][x,y,z,0],u[-l,y,z,t]==u[l,y,z,t],u[x,-l,z,t]==u[x,l,z,t],u[x,y,-l,t]==u[x,y,l,t]},u,{t,0,Tf},{x,-l,l},{y,-l,l},{z,-l,l}, Method->{"MethodOfLines","SpatialDiscretization"->{"TensorProductGrid","DifferenceOrder"->"Pseudospectral"}}]
We look at a plot for a fixed value of t and z. Its a slice of the four dimensional space which is seen.
DensityPlot[Evaluate[u[x,y,0,1]/.dim4],{x,-l,l},{y,-l,l},PlotRange->All,ColorFunction->"DarkRainbow",PlotPoints->40]
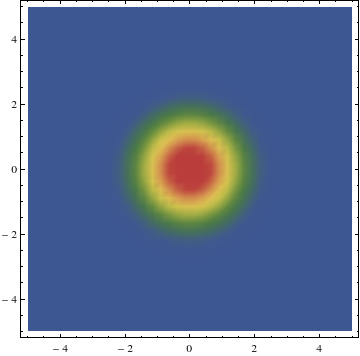
When we try to solve it for larger time intervals we end up with an error as shown below.
l=5;k=1;Tf=2;u4[x_,y_,z_,t_]:=Exp[-x^2-y^2-z^2];dim2=NDSolve[{D[u[x,y,z,t],{t,2}]-D[u[x,y,z,t],{x,2}]-D[u[x,y,z,t],{y,2}]+D[u[x,y,z,t],{z,2}]+u[x,y,z,t]-k (u[x,y,z,t])^3==0,u[x,y,z,0]==u4[x,y,z,0],Derivative[0,0,0,1][u][x,y,z,0]==Derivative[0,0,0,1][u4][x,y,z,0],u[-l,y,z,t]==u[l,y,z,t],u[x,-l,z,t]==u[x,l,z,t],u[x,y,-l,t]==u[x,y,l,t]},u,{t,0,Tf},{x,-l,l},{y,-l,l},{z,-l,l},Method->{"MethodOfLines","SpatialDiscretization"->{"TensorProductGrid","DifferenceOrder"->"Pseudospectral"}}]
We get the follwing error for large time interval.
NDSolve::ndsz: At t == 1.7240917274928276`, step size is effectively zero; singularity or stiff system suspected.
It will be great if some one help me out with this.