Over the past year, I've found it increasingly more difficult to find video games that can keep me entertained. This has forced me to focus more on making my own. Making games was the main reason I got into programming as a teenager (and a popular reason for many, I believe), so it's nice to return to it. For my first game last year, I wanted to make something interesting as quickly as possible. This led me to make a small puzzle game. I prototyped it in Mathematica, and now you can play the JavaScript version here ( www.gatheredgame.com ).
That was a fun exercise, but moving forward, I wanted to create less abstract systems. I'm interested in small fictional worlds, emphasizing intricacy and responsiveness. This would enable player-driven stories, without having to hand-code every possible outcome and without limiting myself to the building and strategy genres. Perhaps things like Dwarf Fortress, but more accessible and varied.
I decided a key to accomplishing this was to more closely tie together the creative writing and programming parts of my design process. I knew that the final result wouldn't hold my attention long enough to be worth the effort if I took the industry approach to game design by starting from an existing genre or game and changing the setting or adding a new feature. Some independent games have been successful by starting from a novel interaction mechanic, and then exploring the language of puzzles that can be generated from that grammar. A prominent example is Portal. I think starting from random creative writing exercises is more fun, but in my initial attempts I had to throw away many details to reduce the results down to something I could start coding. That made the design process feel very inefficient. I want coding a game to feel like creative writing, and I want the output to be interesting from the first few lines until the final result.
Ever since reading NKS, I've been struck by how interesting a random cellular automata browser can be given how little code is required to make one. For example, try enabling rules below until interesting behavior is produced (click the squares to the right of the arrows).
SeedRandom[1];
init = RandomInteger[1, 100]; rule =
Table[False, {2^5}]; Row@{Column@
Table[Row@{Row[
IntegerDigits[a - 1, 2,
5] /. {0 ->
Graphics[{White, EdgeForm[{Thin, Black}], Rectangle[]},
ImageSize -> 10],
1 -> Graphics[{Black, EdgeForm[{Thin, Black}], Rectangle[]},
ImageSize -> 10]}], "\[Rule]",
With[{a = a},
Dynamic@Graphics[
Button[If[
rule[[a]], {{Black, EdgeForm[{Thin, Black}],
Rectangle[]}}, {{White, EdgeForm[{Thin, Black}],
Rectangle[]}}], rule[[a]] = ! rule[[a]]],
ImageSize -> 10]]}, {a, 2^5}], Spacer@10,
Dynamic@ArrayPlot[
CellularAutomaton[{FromDigits[Reverse@Boole@rule, 2], 2, 2}, init,
150], ImageSize -> 350]}

So I decided the easiest way to try and take advantage of the fundamental phenomenon that complex behavior isn't difficult to produce, while simultaneously focusing on concrete objects, was to experiment with association automata. With "association" referring to Wolfram's key/value dictionaries.
I like starting from random story ideas. I currently pull random story tropes from the TV Tropes idea generator to get started. Sometimes I mix in a few random Wikipedia articles.
randomStoryIdea[] :=
DynamicModule[{elements =
Import["http://tvtropes.org/pmwiki/storygen.php", "Data"][[2, 2,
2]]}, Dynamic@
Grid[MapIndexed[{#[[1]],
Hyperlink[#[[2]],
"http://tvtropes.org/pmwiki/pmwiki.php/Main/" <>
StringReplace[#[[2]], Except@LetterCharacter -> ""]],
Button["New",
elements[[#2[[1]]]] =
Import["http://tvtropes.org/pmwiki/storygen.php", "Data"][[2,
2, 2, #2[[1]]]]]} &, elements], Alignment -> Left]]
Here is a random seed I'm working with now:
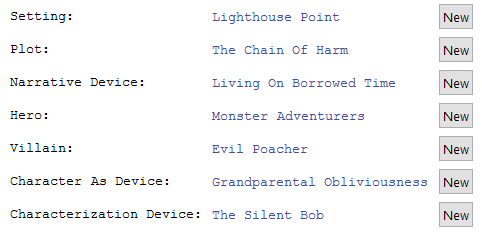
Then I start to stitch some of the elements together in my head. An evil poacher at a lighthouse made me think of a fisherman, perhaps a criminal hiding in a lighthouse who is fishing to survive. Chain of harm and monster adventurers made me think that perhaps his fishing activities are damaging a community of marine life under the dock, and some crabs attempt to stop him. Now I'll start defining some entities and properties. I start with the properties that I think someone would consider most interesting at the end of a game. Health and location of main characters, how many catches did the fisherman complete, what is the state of the crab town?
entities = <|
"fisherman" -> <|"health" -> "healthy", "location" -> "dock",
"catches" -> 0|>,
"hero crab" -> <|"health" -> "healthy"|>,
"assistant crab" -> <|"health" -> "healthy"|>,
"crab town" -> <|"population" -> 50, "crime rate" -> .05|>
|>
Then I define some rules to update those properties, referring to new properties that will influence them. In this way I essentially define the game world by starting from final effects and working backward by defining causes. The entities and properties are defined as an association of associations. The rules are defined as a list of lists that is then converted to associations with some code. Each sublist represents one rule that updates one property of one entity. The first two items of the sublist are the entity and property being updated, and the last item is a pure function that defines the behavior of the rule. Three values are passed to the rule when it is used. Slot[1] is the current value of the property being updated. Slot[2] is the current entity being updated, so I can refer to other properties of that entity easily with #2["property"]. Slot[3] is the association containing the current state of all entities, so I can refer to properties of the fishing rod within a rule that updates the fisherman's catch count with #3["fishing rod","fish on line"].
rules = {
{"fisherman", "health", Which[
#2@"pacemaker" === "off", "dead",
#2@"fear level" >= 30, "dead",
#2@"location" === "ocean", "dead",
#2@"blood level" < 30 && # === "healthy", "injured",
#2@"blood level" <= 0, "dead",
#2@"hunger level" >= 50, "dead",
# === "injured" && #2@"time without bleeding" >= 20, "healthy",
True, #] &},
{"crab town",
"population", # + If[RandomReal[] < #2@"crime rate", -1, 0] +
If[RandomReal[] < #/4*.005, 1, 0] &}
}
Before we look at the behavior of the system, we need to define initial values for any new properties we reference in the rules. Here is some code to find those.
extractVars[fun_, scopedEntity_] :=
Join[Cases[fun, #2[prop_] :> {scopedEntity, prop}, \[Infinity]],
Cases[fun, #3[globalEntity_, prop_] :> {globalEntity,
prop}, \[Infinity]],
Cases[fun,
prop[globalEntity_String, prop_String] :> {globalEntity,
prop}, \[Infinity]]]
Complement[
Union[Join @@ (Prepend[extractVars[#3, #], {#, #2}] & @@@ rules)],
Join @@ KeyValueMap[Thread[{#, Keys@#2}] &, entities]]
The following code expands the rules into associations and allows for simple one-level, OO-style inheritance of properties and rules by using an "is a" property on an entity. This example doesn't utilize that, but the code to apply rules assumes they have been transformed into associations.
(*currently only supports one level of inheritance. inherited rules \
lose ordering*)
fullEntities = entities;
Select[fullEntities, KeyExistsQ@"is a"] //
KeyValueMap[{#, #2@"is a"} &] //
Apply[{entity, parent} \[Function]
AssociateTo[fullEntities,
entity ->
Join[fullEntities@parent, fullEntities@entity]], #, {1}] &;
fullRules =
Select[entities, KeyExistsQ@"is a"] //
KeyValueMap[Cases[rules, {#2@"is a", a__} :> {#, a}] &] //
Select[<|"entity" -> #, "property" -> #2, "rule" -> #3,
If[Length@{##} > 3, "probabilities" -> {##}[[4]],
"probabilities" -> Null]|>, # =!= Null &] & @@@
Join[Catenate@#, rules] &;
Then to step through the evolution of the system, we can use code like the following. In my example the only changes come from a gradually changing population due to birth and crime, so you can use the input field above the step button to take more than one step at a time:
applyRules[entities_, rules_] :=
Fold[ReplacePart[#, {#2@"entity", #2@"property"} -> #2[
"rule"][#[#2@"entity", #2@"property"], #[#2@"entity"], #]] &,
entities, rules]
play[] := (state = fullEntities; steps = 0; stepSize = 1;
Grid[{{Column@{InputField[Dynamic@stepSize, Number, FieldSize -> 4],
Button["Step",
state = Nest[applyRules[#, fullRules] &, state, stepSize];
steps += stepSize], Dynamic@steps},
Dynamic@Column@Normal[state]}}, Frame -> All,
Alignment -> {Center, Center}])
play[]
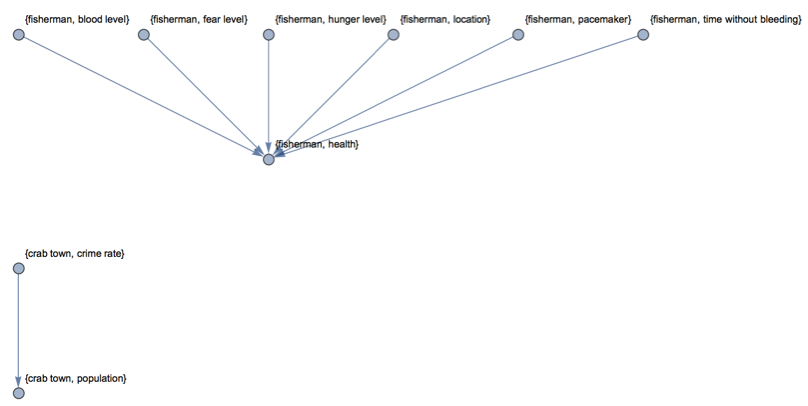
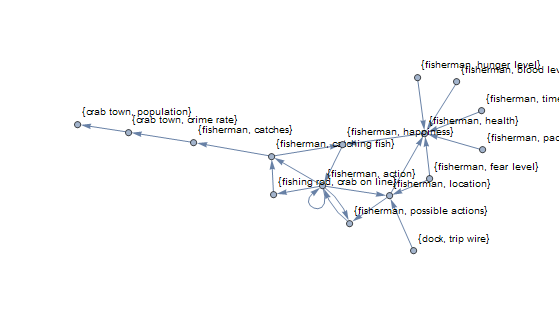
To help decide what rules to add next, I have some code that visualizes which properties influence other properties as a graph, and some code that sorts properties by how many other properties they influence. This makes it easy to add rules that have the greatest downstream effects on the system.
Graph[Flatten[
Thread[Union@extractVars[#[[3]], #[[1]]] \[DirectedEdge] #[[;; 2]],
List, 1] & /@ rules, 1], VertexLabels -> "Name",
PlotRangePadding -> 1]
Module[{counts =
Counts[Join @@ (Union@extractVars[#3, #] & @@@ fullRules)],
counts2 = Counts[Join @@ (extractVars[#3, #] & @@@ fullRules)]},
Complement[
Join[Join @@ KeyValueMap[Thread[{#, Keys@#2}] &, fullEntities],
Keys@counts], Values@fullRules[[All, {"entity", "property"}]]] //
Map[{#, Lookup[counts, Key@#, 0], Lookup[counts2, Key@#, 0]} &] //
SortBy[-Last@# &]]
As you start expanding your system, you'll very quickly realize that defining rules for the behavior of "intelligent" entities in your system is very tedious. I've started investigating some ways to simplify this. We'll use the fisherman as an example, but I plan to use the same techniques for the crabs and others. We can just treat his choice of what action to perform as a search and optimization problem. By giving him a utility or objective property to maximize like "happiness", we can just have him search through a few steps of simulating the system for various possible actions and choose the one that leads to the most happiness.
optimize[property_, choices_, objective_, entities_, rules_,
searchDepth_] :=
Module[{rulesSafe =
Select[rules, property =!= prop[#entity, #property] &]},
First@MaximalBy[
Table[{c,
Module[{newState =
applyRules[ReplacePart[entities, List @@ property -> c],
rulesSafe]},
If[searchDepth > 1,
Last@optimize[property, choices, objective, newState,
rulesSafe, searchDepth - 1], newState @@ objective]]}, {c,
entities @@ choices}], Last]]
You would use that function similar to the following:
{"fisherman", "action",
First@optimize[prop["fisherman", "action"],
prop["fisherman", "possible actions"],
prop["fisherman", "happiness"], #3, fullRules, 5] &}
I gave the fisherman a few possible actions (sitting, standing, casting, fishing, reeling, unhooking) and defined which ones are accessible under which conditions with nested Which expressions. Then I defined his happiness to increase by one whenever he unhooks a fish.
Now we immediately run into a problem where he has no way to prioritize unhooking a fish now when he could just wait a turn and unhook it then. If he is recursively searching two moves ahead, then both unhooking now then waiting or waiting now then unhooking both return the same happiness. So depending on search order, he might just choose to wait every single step. One simple fix for this example is to just multiply his happiness by something like 1.01 at each step. Then he will prioritize unhooking the fish as soon as possible, because ((x+1)1.01)1.01 is greater than ((1.01x)+1)1.01. The sooner he gets happiness increases, the greater the effect of the ongoing multiplier. You could also have his happiness be diminished based on search depth in the optimization recursion, have the formula directly incorporate the amount of time that has passed in the game, etc.
entities = <|
"fisherman" -> <|"health" -> "healthy", "location" -> "dock",
"catches" -> 0, "action" -> "sitting", "happiness" -> 50,
"possible actions" -> {"sitting", "casting", "standing"},
"blood level" -> 100, "fear level" -> 0, "hunger level" -> 0,
"pacemaker" -> "on", "time without bleeding" -> 0,
"catching fish" -> False|>,
"hero crab" -> <|"health" -> "healthy"|>,
"assistant crab" -> <|"health" -> "healthy"|>,
"crab town" -> <|"population" -> 50, "crime rate" -> .05|>,
"fishing rod" -> <|"crab on line" -> False|>,
"dock" -> <|"trip wire" -> "not set"|>
|>;
rules = {
{"fisherman", "action",
First@optimize[prop["fisherman", "action"],
prop["fisherman", "possible actions"],
prop["fisherman", "happiness"], #3, fullRules, 5] &},
{"fisherman",
"catching fish", #2@"action" === "unhooking" && #3["fishing rod",
"crab on line"] &},
{"crab town", "crime rate", .05 + .05*#3["fisherman", "catches"] &},
{"fisherman", "location", Which[
#2@"fear level" >= 20 && # ===
"dock" && #3["dock", "trip wire"] === "set", "ocean",
#2@"action" === "going to lighthouse", "lighthouse",
#2@"action" === "going to dock", "dock",
True, #] &},
{"fisherman", "possible actions", Which[
#2@"location" === "dock", Which[
#2@"action" === "sitting", {"sitting", "casting", "standing"},
#2@"action" === "casting", {"fishing"},
#2@"action" === "fishing", {"fishing", "reeling"},
#2@"action" === "reeling", {"sitting", "unhooking"},
#2@"action" === "unhooking", {"sitting"},
#2@"action" === "standing", {"sitting", "going to lighthouse"},
True, #],
True, #] &},
{"fisherman", "health", Which[
#2@"pacemaker" === "off", "dead",
#2@"fear level" >= 30, "dead",
#2@"location" === "ocean", "dead",
#2@"blood level" < 30 && # === "healthy", "injured",
#2@"blood level" <= 0, "dead",
#2@"hunger level" >= 50, "dead",
# === "injured" && #2@"time without bleeding" >= 20, "healthy",
True, #] &},
{"fisherman", "happiness",
1.01 (# + If[#2@"catching fish", 1, 0] -
If[#2@"health" === "injured", 20, 0]) &},
{"fisherman", "catches", If[#2@"catching fish", # + 1, #] &},
{"fishing rod", "crab on line", Which[
#3["fisherman", "action"] === "fishing" && RandomReal[] < .1,
True,
#3["fisherman", "action"] === "unhooking", False,
True, #] &},
{"crab town",
"population", # + If[RandomReal[] < #2@"crime rate", -1, 0] +
If[RandomReal[] < #/4*.005, 1, 0] &}
};
So now if he was guaranteed to catch a fish within the search depth of his optimization (I'm using 5 for now), he would behave as desired. The problem is that for each step that he is fishing, he only has a 10% chance of a fish biting. This means that almost 9 of 10 times, his optimization search will return no better options than doing nothing. He needs to understand that the chance of catching a fish is always better than doing nothing. I'm experimenting with just manually annotating any rules that depend on randomness. Then I define a new optimization search function that can read these annotations, split the search into multiple branches when necessary, and return the expected happiness from the split. In our example, when he is fishing and no fish has bitten yet, it will return a happiness of .1(the happiness from continuing the search assuming a fish bites)+.9(the happiness from continuing the search assuming a fish doesn't bite).
{"fishing rod", "crab on line",
Which[#3["fisherman", "action"] === "fishing" && RandomReal[] < .1,
True, #3["fisherman", "action"] === "unhooking", False,
True, #] &, {{#3["fisherman", "action"] ===
"fishing" && ! # &, {{.1, True}, {.9, False}}}}}
relevantProbs[rule_, state_] :=
If[KeyExistsQ[rule, "probabilities"],
Select[rule[
"probabilities"], #[[1]][state[rule@"entity", rule@"property"],
state[rule@"entity"], state] &], {}]
applyRulesProb[entities_, rules_] :=
Fold[Function[{states, rule},
Function[state,
If[Length@relevantProbs[rule, state[[2]]] > 0,
relevantProbs[rule, state[[2]]][[1, 2]] //
Map[Function[
branch, {branch[[1]]*state[[1]],
ReplacePart[
state[[2]], {rule@"entity", rule@"property"} ->
branch[[2]]]}]] // Sequence @@ # &, {state[[1]],
ReplacePart[
state[[2]], {rule@"entity", rule@"property"} ->
rule["rule"][state[[2]][rule@"entity", rule@"property"],
state[[2]][rule@"entity"], state[[2]]]]}]] /@ states], {{1.,
entities}}, rules]
optimizeProb[property_, choices_, objective_, entities_, rules_,
searchDepth_] :=
Module[{rulesSafe =
Select[rules, property =!= prop[#entity, #property] &]},
First@MaximalBy[
Table[{c,
Module[{newState =
applyRulesProb[ReplacePart[entities, List @@ property -> c],
rulesSafe]},
If[searchDepth > 1,
Function[branch,
branch[[1]]*
Last@optimizeProb[property, choices, objective,
branch[[2]], rulesSafe, searchDepth - 1]] /@ newState //
Total, Function[branch,
branch[[1]]*branch[[2]] @@ objective] /@ newState //
Total]]}, {c, entities @@ choices}], Last]]
He now displays the desired behavior of choosing to start fishing immediately, waiting until a fish bites, then reeling and unhooking, then continuing.

Right now, the fisherman has perfect knowledge of the system. This is because I pass in the full rules and full set of entities of the system to the optimization search. An interesting next step as I add rules and properties to the system will be to use a subset of the entities and rules that represent his limited mind and knowledge. Then I can add rules that update his knowledge and even his happiness function over time to make him learn. For example, say whether or not a fish bites is actually deterministic based on more detailed rules for crab behavior. However, let's says the fisherman's copy of the system rules excludes those and instead just assumes a 30% random chance of catching a fish. Further, assume the 30% expectation is represented as a property of the fisherman (say "fishing optimism"). Then we can easily add a rule that increases his optimism whenever he catches a fish, and decreases it whenever he doesn't. Then say we add time of day to the system, and expand his happiness function to decrease when he stays out too late fishing. Then he will automatically choose to stay out a little later when he has been a catching a lot of fish compared to when he hasn't been catching many.
That's just one possible extension I've considered. I don't know if this approach will ever lead to me making a commercially successful game, but it's holding my attention for now.