Message Boards

WOLFRAM COMMUNITY

5485 Views

4 Replies

3 Total Likes

View groups...

Follow this post

Share this post:

GROUPS:

Mathematics Mathematica Algebra

Can this equation system be solved?

Fred Alstair

Posted 9 years ago

12500/13 * 13^(x/5)== y * 2 * 10^07 * 4^((y - 175)/25) * 2.76 * 10^07 * d * 0.03 y = Log[1.07, -((z/(6.510^9)) (1 - 1.07)/1.07)] z = 301 * d * 0.01 * 11400 * -(13^((x/5) + 1)/(1 - 13)) d > 0 x > 0 trying to find f(d)= some value of x if you replace d with a value it will give the right answer, but i cant find the formula for any d for example /.d -> 37878 give the right answer x -> 309.583 but trying for a general solution only give a solution where either d or x is negative

POSTED BY: Fred Alstair

4 Replies

Sort By:

Fred Alstair

Posted 9 years ago

thank you, that was really helpful, though before seeing your solution i did find one of my own though less elegant : pointList = Table[f = y210^074^((y - 175)/25)6.6510^04 d 0.03((d/33100)/25/810 + 1)((d/33100)/25/75 + 1); y = Log[1.07, -((z/(6.510^9))(1 - 1.07)/1.07)]; z = 58.82 ((d/33100)/25/810 + 1) d0.0111400-(13^((x/5) + 1)/(1 - 13)); V1 = Solve[{f == 12500/1313^(x/5)}, x]; {d, x /. V1[[2]]}, {d, 100, 50000, 100}] the code change a bit since i posted it there's also 2 point that appear to be wrong not sure how they got there

thank you, that was really helpful, though before seeing your solution i did find one of my own though less elegant :

pointList = 
 Table[f = 
   y*2*10^07*4^((y - 175)/25)*6.65*10^04 * 
    d *0.03*((d/33*100)/25/810 + 1)*((d/33*100)/25/75 + 1);
  y = Log[1.07, -((z/(6.5*10^9))*(1 - 1.07)/1.07)];
  z = 58.82* ((d/33*100)/25/810 + 1)*
    d*0.01*11400*-(13^((x/5) + 1)/(1 - 13));
  V1 = Solve[{f == 12500/13*13^(x/5)}, x];
  {d, x /. V1[[2]]}, {d, 100, 50000, 100}]

the code change a bit since i posted it there's also 2 point that appear to be wrong not sure how they got there
enter image description here

POSTED BY: Fred Alstair

Shenghui Yang

Shenghui Yang, WOLFRAM

Posted 9 years ago

The equation you are solving is transcendental so usually it does not have a simple solution from `Solve` function. Also once you have numeric coefficients in the equation, I think `NSolve` is used automatically. The reason that you have two solutions from your code is the `Log` function used for `z` works on complex plane or the negative arguments, you just encountered a complex root there. I modified the solver in your code with the `FindRoot` function so that the only real solution is guaranteed to be spotted on. Use `ReplaceAll` (//.) to save some variables. Clear["Global`"] f = y210^074^((y - 175)/25)2.7610^07 * d 0.03 //. {y -> Log[1.07, -((z/(6.510^9))(1 - 1.07)/1.07)], z -> 301 d0.0111400-(13^((x/5) + 1)/(1 - 13))}; I use `Log` function to map the `f` and the equation that you are solving onto the logarithmic plane so that the solution converges fast. h1[x_, d_] = FullSimplify[f, Assumptions -> {x \[Element] Reals, d \[Element] Reals}] (80704. d^1.81958 E^(0.420437 x) Log[3.741410^-7 13^(x/5) d]) h2[x_, d_] = N@PowerExpand@(Log[h1[x, d]] - Log[12500/1313^(x/5)]) (1.86506 - 2.56495 (-1. 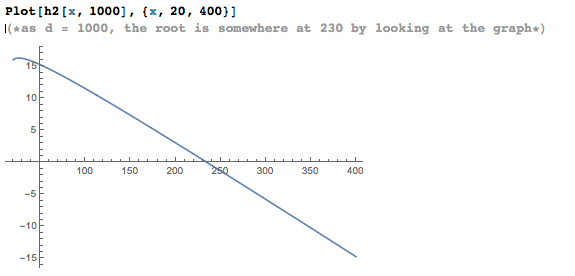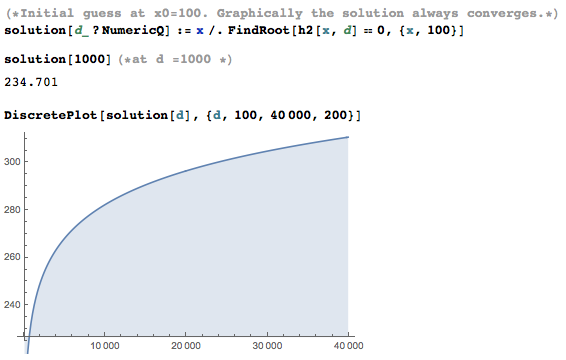+ 0.2 x) + 0.420437 x + 1.81958 Log[d] + Log[-14.7986 + 0.51299 x + Log[d]]) (with small x, the value of h2 can be complex that is why you have \two solutions) h2[10, 1000] ( result = 17.0893 + 3.14159 I) Given `d=1000`, we can find the root of `h2` by `Plot` function and the intersection between the curve and the x axis: We can define a function `solution` to find the root programmatically: The code is attached with this reply in `wall2_Mod.nb` Attachments:*