The equation you are solving is transcendental so usually it does not have a simple solution from Solve function. Also once you have numeric coefficients in the equation, I think NSolve is used automatically. The reason that you have two solutions from your code is the Log function used for z works on complex plane or the negative arguments, you just encountered a complex root there. I modified the solver in your code with the FindRoot function so that the only real solution is guaranteed to be spotted on.
Use ReplaceAll (//.) to save some variables.
Clear["Global`*"]
f = y*2*10^07*4^((y - 175)/25)*2.76*10^07 * d *0.03 //.
{y -> Log[1.07, -((z/(6.5*10^9))*(1 - 1.07)/1.07)],
z -> 301 *d*0.01*11400*-(13^((x/5) + 1)/(1 - 13))};
I use Log function to map the f and the equation that you are solving onto the logarithmic plane so that the solution converges fast.
h1[x_, d_] =
FullSimplify[f,
Assumptions -> {x \[Element] Reals, d \[Element] Reals}]
(*80704. d^1.81958 E^(0.420437 x) Log[3.7414*10^-7 13^(x/5) d]*)
h2[x_, d_] = N@PowerExpand@(Log[h1[x, d]] - Log[12500/13*13^(x/5)])
(*1.86506 - 2.56495 (-1. + 0.2 x) + 0.420437 x + 1.81958 Log[d] + Log[-14.7986 + 0.51299 x + Log[d]]*)
(*with small x, the value of h2 can be complex that is why you have \two solutions*)
h2[10, 1000] (* result = 17.0893 + 3.14159 I*)
Given d=1000, we can find the root of h2 by Plot function and the intersection between the curve and the x axis:
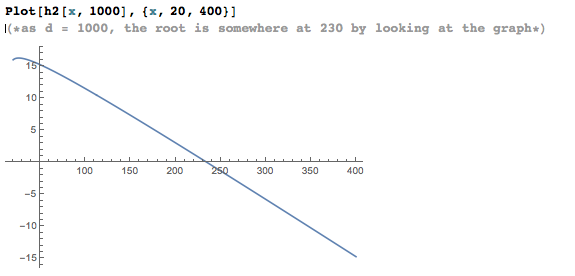
We can define a function solution to find the root programmatically:
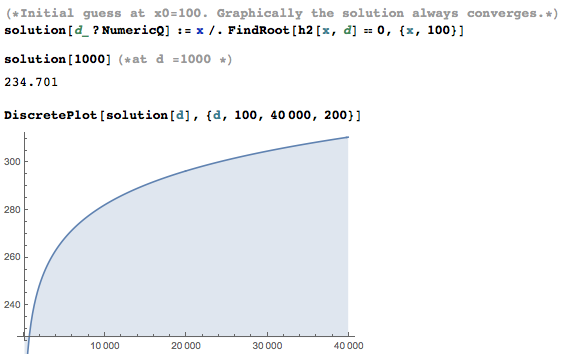
The code is attached with this reply in wall2_Mod.nb
 Attachments:
Attachments: