Hi,

if the image is assigned to the variable img, then

ImageMultiply[
 Erosion[DeleteSmallComponents[
   GeodesicClosing[
    GeodesicOpening[
     AlphaChannel@RemoveBackground[img, {"Foreground", Brown}], 15], 
    10], 100], 8], img]

gives

DeleteSmallComponents[ ImageMultiply[ Erosion[DeleteSmallComponents[ GeodesicClosing[ GeodesicOpening[ AlphaChannel@RemoveBackground[img, {"Foreground", Brown}], 15], 10], 100], 8], img], 1200]

removes the small components.

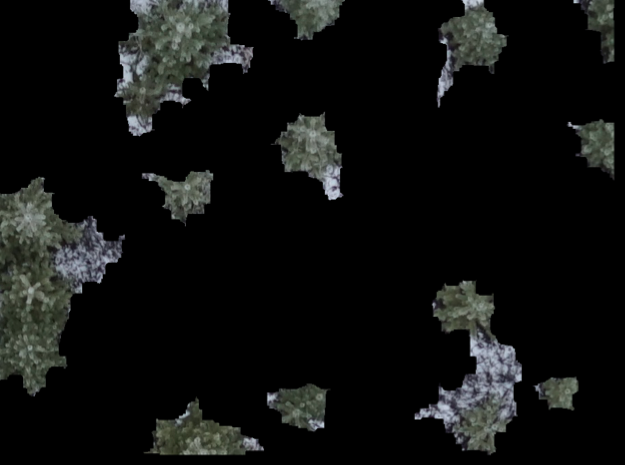
If you want a white background use:

RemoveBackground[
 DeleteSmallComponents[
  ImageMultiply[
   Erosion[DeleteSmallComponents[
     GeodesicClosing[
      GeodesicOpening[
       AlphaChannel@RemoveBackground[img, {"Foreground", Brown}], 15],
       10], 100], 8], img], 1200], {"Background", "Uniform"}]

You can colorise the individual trees (note that it doesn't work right for two close trees in this image):

MorphologicalComponents[
  RemoveBackground[
   DeleteSmallComponents[
    ImageMultiply[
     Erosion[DeleteSmallComponents[
       GeodesicClosing[
        GeodesicOpening[
         AlphaChannel@RemoveBackground[img, {"Foreground", Brown}], 
         15], 10], 100], 8], img], 1200], {"Background", 
    "Uniform"}]] // Colorise

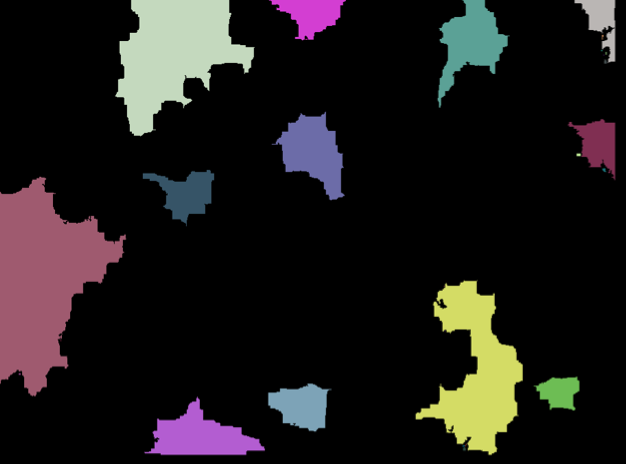
This here would count the trees (at least approximately):

Length[Select[
  ComponentMeasurements[
   MorphologicalComponents[
    RemoveBackground[
     DeleteSmallComponents[
      ImageMultiply[
       Erosion[DeleteSmallComponents[
         GeodesicClosing[
          GeodesicOpening[
           AlphaChannel@RemoveBackground[img, {"Foreground", Brown}], 
           15], 10], 100], 8], img], 1200], {"Background", 
      "Uniform"}]], "Area"], #[[2]] > 1000 &]]

In this case it gives 12 which corresponds to the large coloured areas in the last image. Hence, it only counts well separated trees.

Cheers,

Marco

Hi Marco and Henrik,

Both approaches are fantastic to me! I really want to study both of your codings.

Again, thank you very much!

Eiji