Hi,

that is the step by step solution. This also works:

FullSimplify[1/2 Log[x + 2] - (Evaluate@Integrate[1/(2 x + 4), x]), Assumptions -> x > -1]

It gives

-(Log[2]/2)

so a constant which obviously equals

-(-(Log[2]/2) + Log[4]/2)

You can also do:

1/2 Log[x + 2] + Log[2]/2 == (Evaluate@Integrate[1/(2 x + 4), x]) // FullSimplify

or evaluate the derivatives:

FullSimplify[D[1/2 Log[x + 2], x] == D[(Evaluate@Integrate[1/(2 x + 4), x]), x]]

Cheers,

M.

Dear Rodrigo,

that's a kind of problem that comes up from now to then. It is true that the two results look different (and are up to a constant). If you plot the functions they do look different:

Plot[{1/2 Log[x + 2], Evaluate@Integrate[1/(2 x + 4), x]}, {x, -5, 6}]

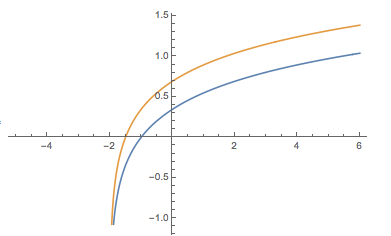
They are obviously not identical. I will argue that they are still the same up to an additive constant.

Let's look at WolframAlpha's solution the the solution that you got from the other program (and that I got from Mathematica using Integrate); I'll evaluate the difference for some arbitrary value, here $x=0$:

(1/2 Log[x + 2] - (Evaluate@Integrate[1/(2 x + 4), x])) /. x -> 0

We get

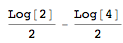
If we subtract that appropriately we get:

Plot[1/2 (-2 (Log[2]/2 - Log[4]/2) + Log[2 + x] - Log[4 + 2 x]), {x, -15.5, 11.5}]

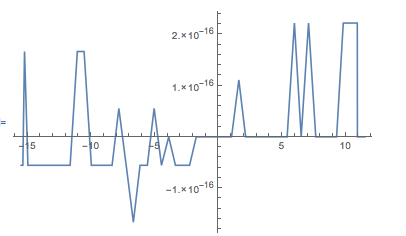
That's what we can call a "numerical zero". We can now do that more rigorously:

FullSimplify[1/2 Log[x + 2] - (Log[2]/2 - Log[4]/2) - (Evaluate@Integrate[1/(2 x + 4), x])]

evaluates to zero. So the two solutions are identical up to an additive constant.

Cheers,

Marco