This discussion is inspired by the question from a Mathematica user. The post involves decent vector calculus and Mathematica code so it deserves a designated page for the presentation. Besides the mathematical challenge, I also comprehensively use advanced Wolfram technologies such as Wolfram Alpha with nature language processing, geographic database, real world entities and Mathematica's powerful visualization capability (like the gauge GUI).
Please download the attached notebook to run all the code snippets. Feel free to play around the technology here and hopefully you will learn more about how to use these great features of the Wolfram platform.
The problem states the following
Find the location on the surface of earth where the moon sits at zenith, given the moon's position at the observers location (in terms of azimuth and altitude angle)
Conclusion
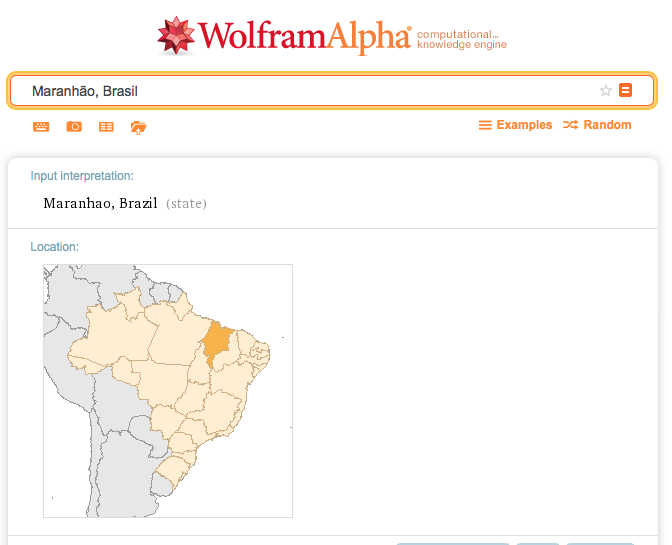
On 2/25/2016 at 23:30 Chicago time zone, the people, who reside at the location shown on the map, see the moon right above their head. In scientific term, the altitude of the moon position at the location is 90 degree.
Analysis
Since the position of moon is changing as time goes by, I would like to use the following function to take a snapshot of the motion at
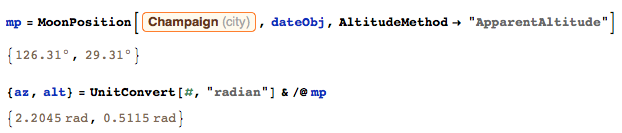
dateObj = DateObject[{2016, 2, 25, 23, 30}] (* The moment that I started to write this blog *)
The moon position from my view at the city of Champaign, IL:
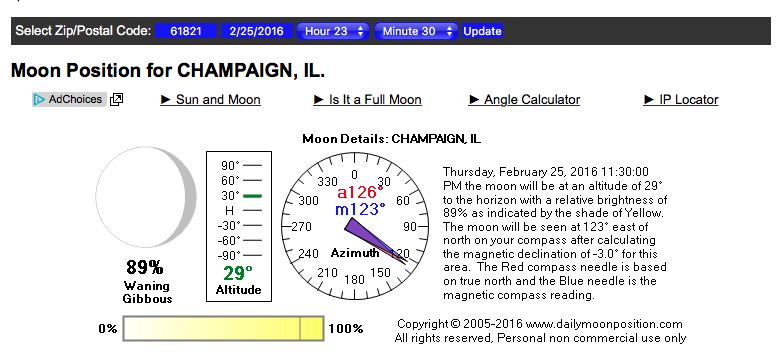
You can check the result from Daily Moon Position as well. This is the screenshot of the result online at the given location and time spot. The zip codes of Champaign IL includes 61821
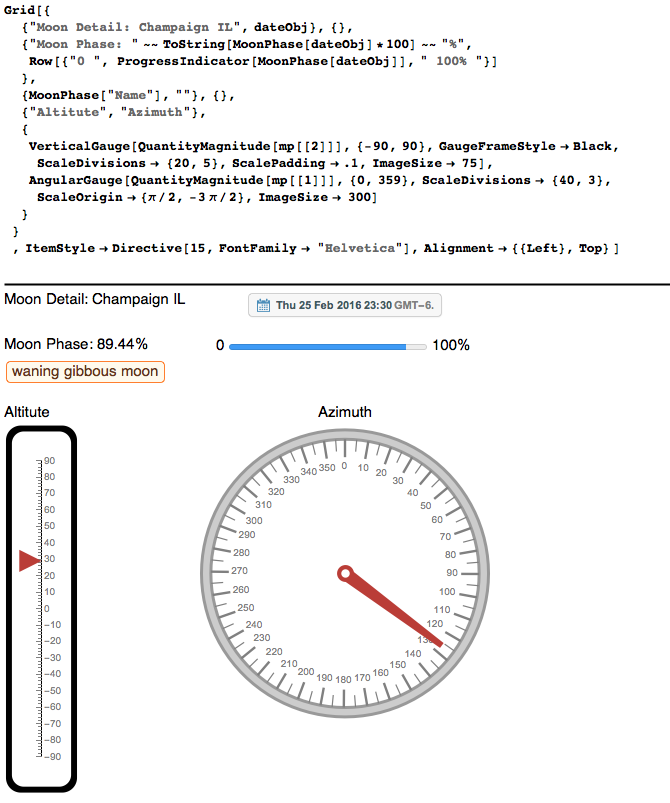
We can visualize the above results using the Mathematica powerful UI controls. In the azimuth meter, 0 denotes the true north; 180 the sourth; 90 the east; 270 the west. You can imagine that this compass is put on the ground or on the tangential plane of the earth at a particular instance. In my case , it is Champaign, IL . This Mathematica GUI is more visually pleasant than the previous screenshot.
The idea to solve this problem is to use the coordinate tranformation: convert the coordinate of the moon in the frame of the local observer to the space cartesian coordinate. Meanwhile, we convert, again, the coordinate of the moon from the earth's sperical coordicate to the same Cartesian system. We equate the two expressions to find the right values of the latitude and longitude of the location where the culmination of the moon is observed. Then we shall check the moon position at the output location to see if the altitude is 90 degree.
The flow of analysis is

To solve the problem we also need the geo location of Champaign IL :

I will use the (radius, arithmus, polar) convension that is applied throughout on this page: http://mathworld.wolfram.com/SphericalCoordinates.html.
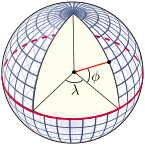
The convension is such that the cartesian center coincides with the center of the earth. Meanwhile, the x-axis of the coordinate passes through the intersection of prime meridian and equator. The y axis passes through the intersection of 90th meridan east and equator. The z-axis points to north pole. The diagram for longitude ( $\lambda$) and latitude ( $\phi$) is shown on the diagram (Source):
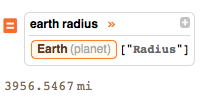
Thus, given the geo position of my local spot, I can obtain the new coordinate by CoordinateTransformData function. The radius is simply the average radius of the earth. I can extract the value from the Wolfram Database for astronomy automatically
Convert the result to pure number. One thing to mention here the polar angle used in CoordinateTransformData function is the complementary angle of the latitude, aka ( $\pi/2 - $ latitude)

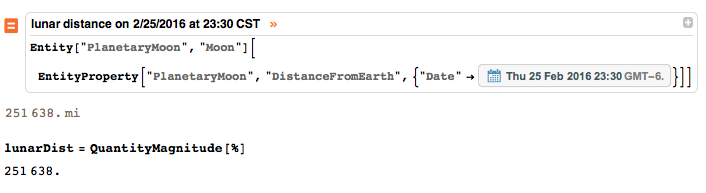
We can also find the distance from the center of the earth to the center of the moon using the following query. If you query "distance from earth to moon " you might have a different result because Wolfram Alpha use the current time frame to retrieve the information or it simply return the average distance.
These are the bases in the Cartesian coordinate:
basis = {e1, e2, e3};
By quite complicated spacial coordinate transformation,

we have the following operator:
trfM[\[Lambda]_, \[Phi]_] := {{-Sin[\[Lambda]], Cos[\[Lambda]],
0}, {-Sin[\[Phi]]*Cos[\[Lambda]], -Sin[\[Phi]]*Sin[\[Lambda]],
Cos[\[Phi]]}, {Cos[\[Phi]] Cos[\[Lambda]],
Cos[\[Phi]] Sin[\[Lambda]], Sin[\[Phi]]}}
The conversion from observer's basis to the cartesian basis is the inner product we have below:
trfM[a,b].basis
{e2 Cos[a]-e1 Sin[a],e3 Cos[b]-e1 Cos[a] Sin[b]-e2 Sin[a] Sin[b],e1 Cos[a] Cos[b]+e2 Cos[b] Sin[a]+e3 Sin[b]}
Now lets take a look at the coordinate of the moon in the observer's frame:

where l is the distance between my location and the center of the moon, theta is local altitude and psi is the local azimuth angle.Use the conversion routine we have just discussed, we can obtain the cartesian coordinate of the moon:

Extract the coefficient of the e1, e2 and e3. These coefficient is exactly the so-called x-y-z component of the moon's position in space.
rhs=Coefficient[newCoord,#,1]&/@basis
(* {91.1542 +0.723664 l,-3024.4-0.685557 l,2549.3 -0.0795132 l} *)
If we want to describe the coordinate of the moon in our Cartesian systems, we have to use TransformationFunctionData again:
MoonCoord=lhs=CoordinateTransformData["Spherical"->"Cartesian", "Mapping", {lunarDist,Pi/2-moonLat,moonLon}]
(* {251638. Cos[moonLat] Cos[moonLon],251638. Cos[moonLat] Sin[moonLon],251638. Sin[moonLat]}*)
Back to the beginning of our solving scheme, the moon's spactial location is invariant regardless of where the cartesian description is transformed from. This is illustrated in the diagram below:
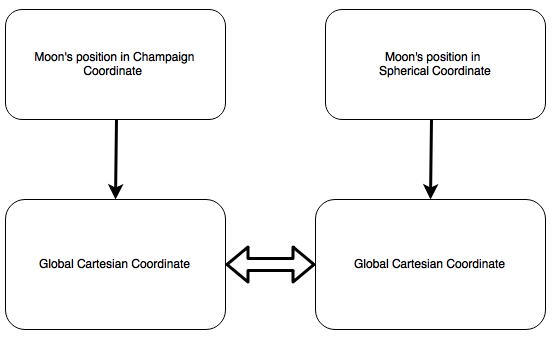
Thus we have three equations: x = x, y = y, z = z. And three unknowns: moonLat, moonLon and l = distance between Champaign IL and the center of the moon.
sol=FindRoot[Thread[rhs==lhs],{moonLat,0},{moonLon,0},{l,lunarDist}]
(* {moonLat->-0.0688172,moonLon->-0.76686,l->249678.} units: {radian, radian, mile}*)
Convert the result back to the geo location:
location=GeoPosition[180/Pi*{moonLat,moonLon}/.sol]
(* GeoPosition[{-3.94294,-43.9378}] *)
MoonPosition[%,DateObject[{2016,2,25,23,30}]]
(* {91.60 Degree ,89.02 Degree } *)
Since the altitude is almost 90 degree, I think the result is fairly close. Visually verify the result with the sky chart generated from Wolfram Alpha. It shows that the moon is about at the zenith over the computed location.
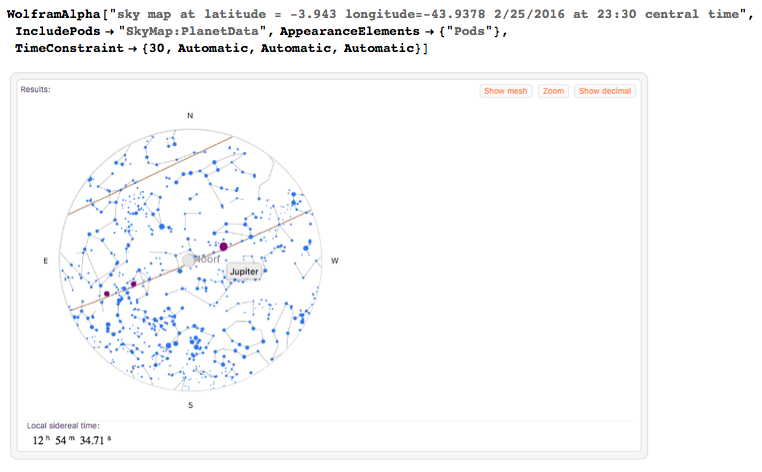
One thing worth to mention here is that the equation we have solved. It could have two solutions. The geometric interpretation of the solutions is the location on the earth colinear both with the center of the earth and moon. This line connecting the center of both planets will touch the surface of earth twice. So you want to check if the moon is above head or beneath the foot.
A few extra things with Wolfram Alpha
- Where is the spot we have just found on the earth?
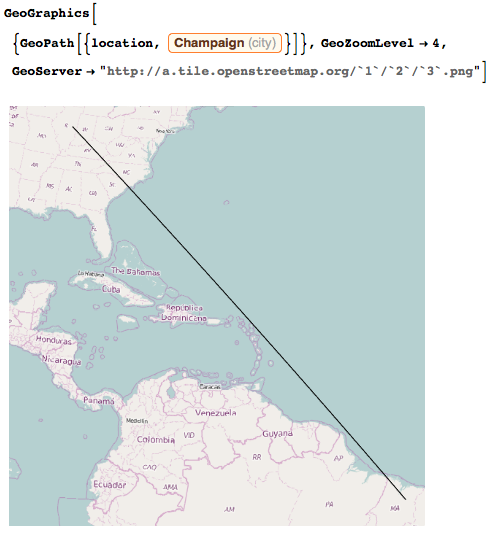
How far away is it from Champaign IL? 1/6 of earth circumference is not a short distance!
WolframAlpha["distance between champaign and latitude = -3.943 longitude = -43.9378",{{"FractionOfEarthCircumference",1},"ComputableData"}]
0.17 ~~ 1 / 6
Any popular place near the site?
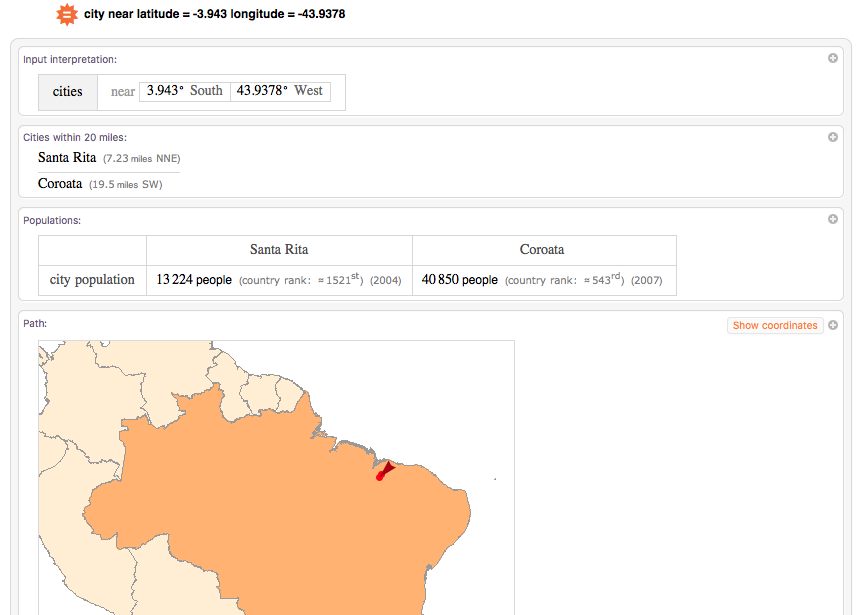
Further Readings