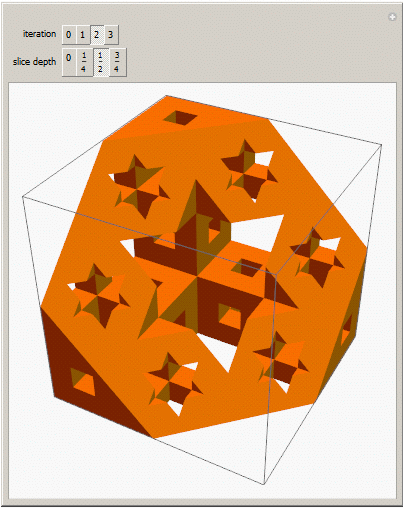
In the Menger sponge, a step divides a cube into 27 cubes, then the center and six touching cubes are removed. Here's what it looks like after three steps.
Graphics3D[
Cuboid /@ ((FromDigits[#, 3] & /@ Transpose[#]) & /@
Select[Partition[#, 3] & /@ Tuples[Range[0, 2], {9}],
Max[Count[#, 1] & /@ #] < 2 &]), Boxed -> False]

You can also take slices, as shown in the Wolfram Demonstration Menger Sponge Slices.
A string rewriting system gives a related fractal known as the Sierpi?ski Carpet. It is a face of the Menger sponge. Here are two different pieces of code to generate it.
Row[{ArrayPlot[
Table[If[
Not[MemberQ[
Transpose[(IntegerDigits[#, 3, 5] & /@ {a, b})], {1, 1}]], 1,
0], {a, 0, 3^5 - 1}, {b, 0, 3^5 - 1}], PixelConstrained -> True,
ImageSize -> 250], Spacer[20],
ArrayPlot[
Nest[ArrayFlatten[# /. {0 -> {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}},
1 -> {{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}}, 2] &, {{1}}, 5],
Frame -> False, PixelConstrained -> True, ImageSize -> 250]}]
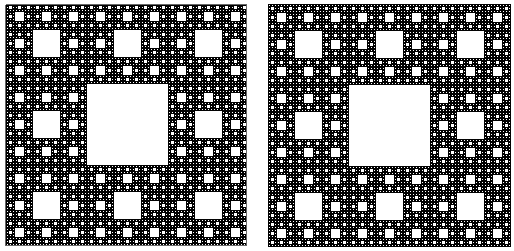
Taking a horizontal line through the center gives the Cantor set (also known as the middle-thirds set), an infinite closed perfect set of zero measure.

You might recognize the ternary (base 3) numbers in each set of code. For the 1D Cantor set, remove any ternary number with a 1. For the 2D Sierpinski carpet, if the nth ternary digits are both 1, remove that pair of numbers. For the 3D Menger sponge, if two or three of nth ternary digits are1, remove that triplet of numbers. All of these objects tend to a set of measure zero, whether the measure is length, area, or volume.
So those are ways to get measure 0 with a fractal. How about making Pi with a fractal? These two infinite products look promising for 1D.
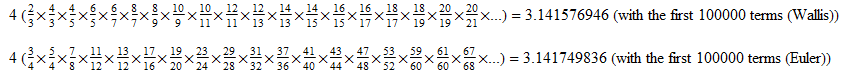
Transforming the fractions into fractals requires adding a segment when the fraction is greater than 1. Here's what the fractals look like after a few steps, followed by a check to make sure the segment lengths are adding up correctly.

I shall call the first of those the happy Pi fractal. To be more bold about it, here are those formulas again.
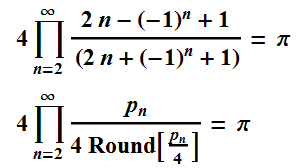
Plotting the values given by these fractals gives something that looks like the Minkowski ? function, which is based on the Farey sequence of irreducible fractions. Build circles of radii twice the denominator squared above each fraction to obtain the Ford circles, a fractal of tangent circles.
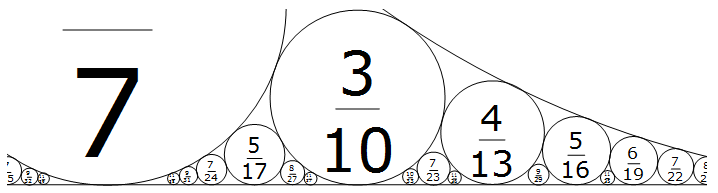
An irreducible fraction a/b in the Farey sequence has gcd(a,b)=1 and a less than b. It happens that the probability of random integers being relatively prime with a less than b is 3/Pi^2. We can use that to approximate the length of F1422, all the irreducible fractions with denominator of 1422 or less. Out of a 1422*1422 grid of pixels, about 3/Pi^2percent of them should be black.

By squaring 1422 and multiplying we should be able to get a reasonable approximation for the size of F1422. Then we can check to find the actual size.
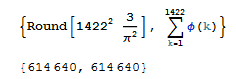
Fairly accurate, but enough with 1D. For a 2D fractal for Pi, we can use the Wallis product again.
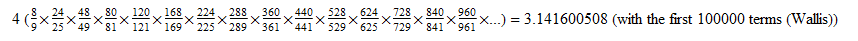
The corresponding fractal is the Wallis sieve.
Start with a 2*2 square and divide it into 4 squares.
Divide each new subsquare by 3, and remove the middle square (8/9).
Divide each new subsquare by 5, and remove the middle square (24/25).
Divide each new subsquare by 7, and remove the middle square (48/49).
Divide each new subsquare by 9, and remove the middle square (80/81).
And so on. Here's what it looks like after a few steps.
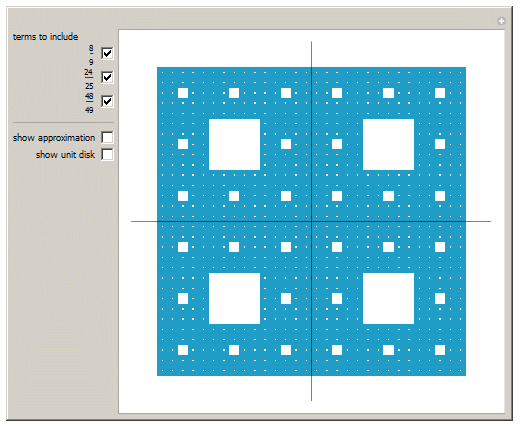
As mentioned earlier, this fractal has an area equal to Pi.
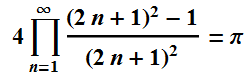
Is there a Menger sponge equivalent of the Wallis sieve? At each step, we'd divide the remaining cubes into the next largest odd cube, then take away the cubes extending out from the center.
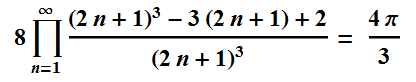
That's the same volume as a sphere of radius 1. What would one of these fractals look like? The code is similar: getting the digits 1, 2, or 3 in bases 3, 5, or 7 more than once causes a triplet to get tossed out.
wallissponge = Select[Tuples[Select[Tuples[Range[0, 6], {3}], Sign[{3, 5, 7} - #] == {1, 1, 1} &], {3}],
Max[MapIndexed[Count[#1 - #2[[1]], 0] &, Transpose[#]]] < 2 &];
Graphics3D[{EdgeForm[None], Cuboid /@ ((5 7 #[[1]] + 7 #[[2]] + #[[3]] & /@ # ) & /@ wallissponge)}, Boxed -> False, ImageSize -> 600]

Use eight of these to get a fractal object with the same volume as the unit sphere.
We've taken some fractals of measure zero and tweaked them a bit to get Pi. If anyone can break this fractal into pieces and make a sphere, please let me know.
 Attachments:
Attachments: