Introduction

This past summer, between my sophomore and junior years of high school, I attended the Wolfram High School Summer Camp (Mathematica Track). Although I had briefly used the Wolfram Language previously, this was my first real experience with the system. During those two weeks, I worked on a project while meeting lots of very inspiring people, incluing Stephen Wolfram.

A few months later, I was offered the opportunity to participate in the Wolfram Mentorships program. On the list of available projects, "Personal Timeline Visualization" intrigued me. I always liked working on projects that appealed to wide varieties of people, so this one was especially compelling to me.

Initial Coding

It was fairly easy to create a simple time line that plotted Instagram posts chronologically. Each photo in a user's "feed" was represented by a dot with the image as their tooltip. This code can be see below:

instagram=ServiceConnect["Instagram"]
images=(First[instagram["LatestMedia","UserID"->#]])&/@instagram["FollowingIDs"]
date=instagram["CreationDate","MediaID"-> #]&/@((Flatten@DeleteCases[StringCases[instagram["LatestMediaIDs","UserID"->#],RegularExpression["[[:digit:]]+_[[:digit:]]+"]],{}]&/@instagram["FollowingIDs"])[[All,1]])
TimelinePlot[(Tooltip[#[[1]],#[[2]]]) & /@ Transpose[{date,images}]]

After experimenting with various other social media services (including Twitter, Pushbullet, and Flickr), I decided to primarily focus on Instagram. This was because it had by far the largest amount of available options. After thinking some more about where to take the project next, I decided that I would like to look for trends. I use social media mainly to communicate with people, but I have always liked the ability to see what the world was "talking" about, and seeing if there were patterns in Instagram posts over time seemed interesting to me.

Using some of by past experience from my Wolfram High School Summer Camp, I created a globe using Graphics3D, the code for which can be seen here:

globe=SphericalPlot3D[3956.5467,{u,0,Pi},{v,0,2Pi},Mesh->None,TextureCoordinateFunction->({#5,1-#4}&),PlotStyle->Directive[Specularity[None],Texture[INSERTIMAGEHERE],Axes->False,Background->Black,RotationAction->"Clip",Boxed->False,Lighting->"Neutral"];

After that, images were plotted using the globe, connected by dotted lines. Thus, if one were to follow a bunch of popular Instagram accounts, it would be possible to see where they were based. For example, after following a bunch of popular #Surfing accounts, it appeared that most of the photos appeared from Australia (not too surprising!). It appears in general, the majority of "Trending" accounts orginiate mainly from the United States (also not too surprising). The code inside the full notebook can be found below. However, the "Elements"-> Images parameter is new in Mathematica Version 10.4, so you will get errors if compiling with an earlier version (although it is still usable to an extent).

Instagram = ServiceConnect["Instagram"];
InstagramImages = (Instagram[
       "LatestMedia", {"UserID" -> #, MaxItems -> 1, 
        "Elements" -> "Images"}][[1]]) & /@ 
   Instagram["FollowingIDs"];
InstagramDates = (Instagram["CreationDate", 
      "MediaID" -> #] &) /@ (First[
       Instagram["LatestMediaIDs", "UserID" -> #]] &) /@ 
    Instagram["FollowingIDs"];
InstagramLocations = (Instagram["Location", 
      "MediaID" -> #] &) /@ (First[
       Instagram["LatestMediaIDs", "UserID" -> #]] &) /@ 
    Instagram["FollowingIDs"];
CoreData = DeleteCases[
   Transpose[{InstagramImages, 
     DateList[#] & /@ InstagramDates, {"latitude", "longitude"} /. 
      InstagramLocations}],
   {_, _, {"latitude", "longitude"}}];
CoreGeoData = {GeoMarker[GeoPosition[#[[3]]], #[[1]]], #[[2]][[
      3]]} & /@ CoreData;
globe = SphericalPlot3D[1, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, 
   TextureCoordinateFunction -> ({#5, 1 - #4} &), 
   PlotStyle -> 
    Directive[(*Specularity[None],*)Texture[INSERTIMAGEHERE]], 
   Axes -> False, Background -> White, RotationAction -> "Clip", 
   Boxed -> False, Lighting -> "Neutral"];
Manipulate[
 Show[globe, Graphics3D[#[[1]]
      /. GeoMarker[GeoPosition[{lat_, lon_}], i_] :> 
       With[{point = 
          Normalize[
           GeoPositionXYZ[GeoPosition[{lat, lon - 180}]][[1]]], 
         factor = 1.3}, {{Dashed, Opacity[0.8], 
          Line[{point, (factor - .1) point}]}, 
         Inset[ImageResize[i, 25], factor point]}] & /@ 
    Select[CoreGeoData, #[[2]] == day || all == True &]]], {day, 1, 
  31, 1}, {all, Checkbox}]

If everything works you should be able to see everything on the globe, like it is below!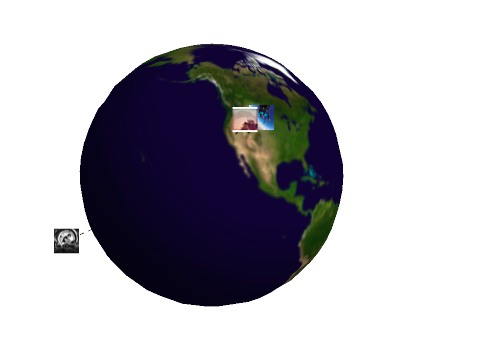

You can see a quick video of this at: https://youtu.be/bozUYe70yAQ.

Challenges Faced

I would say this project proved to be the most challenging at the beginning, mostly because my only prior experience to the Wolfram Language was at Wolfram High School Summer Camp (which I highly recommend!). Overall, I would say the most difficult part was managing the list which combined images with their dates. Graphics proved interesting as well, and I discovered that it can hard to manage an object that has lots of parameters.

Conclusions

I enjoyed working on this for a few reasons. First and foremost, it gave me the opportunity to learn a lot about the Wolfram Language. Second of a all, I think this is a good demonstration of what the program can do. I think that Mathematica is mainly seen as software used to solve difficult math problems, but this proves that it can be applied to a very wide variety of subjects, social media and graphics being one of them. I was very impressed with what the Wolfram Language is capable of doing with just a few lines of code. Ideas for future improvements to this project would be to add the ability to search for images via hash tag, which would enable the visualization of specific global events.

Overall, this was a great learning experience for me and I really enjoyed working on this project. I would like to graciously thank Alison, Christian, and Wolfram Language for helping me with the project as well as exposing me to the Wolfram Language, which I know I will be incorporating into my schoolwork in the future.