Well, the particular example you give is a bit boring, because the two sin functions have have the same frequency (sorry for this incorrect way of expressing this...), but this would work:

Play[2 Sin[440 2 Pi t] 20 Sin[440 2 Pi t], {t, 0, 1}]

So the idea is that you multiply the sine functions and not the Play functions. Play produces a nice "sound object" which a graphical interface and all. What you are doing is multiplying the output of that.

Cheers,

Marco

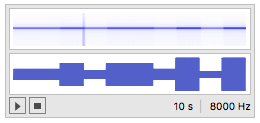
Well, what have you tried? The most obvious thing would be to try and multiply the Sin with some sort of time dependent amplitude such as:

Play[1/(t + 1)*Sin[440 2 Pi*t], {t, 0, 10}]

which works just fine.

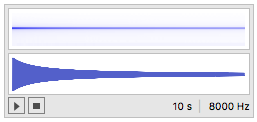
Of course you can multiply by any time dependent amplitude:

Play[Cos[2 Pi t]*Sin[440 2 Pi*t], {t, 0, 10}]

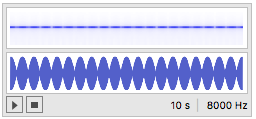
Cheers,

Marco

This might also be useful:

Play[Evaluate[Sin[440 2 Pi*t] Evaluate[Which @@ Evaluate[Flatten[{#[[1]] <= t <= #[[2]], 1./RandomInteger[{2, 10}]} & /@ Transpose[{Range[0, 9], Range[1, 10]}]]]]], {t, 0, 10}]