Here's another one over the reals. The idea is very similar to S M Blinder's approach - we have to deal with an integral that Mathematica does not appear to like.

Plot[Sign[Sin[Pi 2^x]], {x, 0, 10}, PlotPoints -> 5000]

This function oscillates faster and faster, and jumps from -1 to +1.

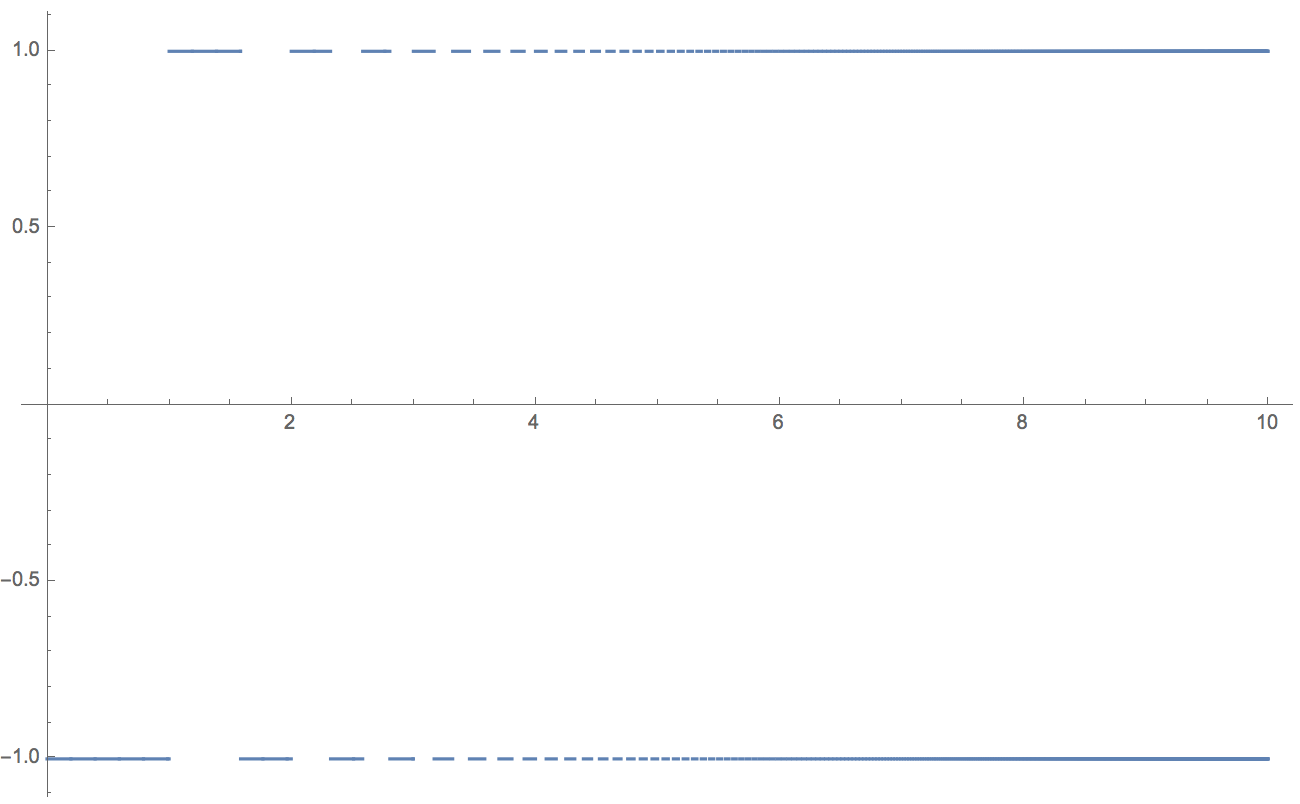
So it obviously does not converge. It turns out that Mathematica cannot directly integrate this to infinity. We can only get the first couple of steps:

Table[Integrate[Sign[Sin[Pi 2^x]], {x, 0, k}], {k, 1, 4}]

or

N[%]
{-1., -0.830075, -0.741434, -0.696551}

But it can determine the roots of the sin function.

Reduce[Sign[Sin[Pi 2^x]] == 0 && x \[Element] Reals, x]

Between the zeros the function is constant -1 or 1. Note that the zeros are between consecutive $\log(k)/\log(2)-\log(k+1)/\log(2)$ so we can calculate the Integral as the limit of the following sum:

Limit[Sum[(-1)^(k + 1) (Log[ k]/Log[2] - Log[1 + k]/Log[2]), {k, 1, j}], j -> Infinity]

which evaluates to

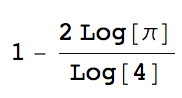
or -0.651496.

So, the integral is finite and the function does not converge. The example given by S M Blinder is easier, because Mathematica evaluates the integral, but I found this example also instructive, because we solve it without using direct integration. (At least if I haven't made a mistake somewhere.)

My feeling is that this is the right result. There is, however, this calculation:

Integrate[Sign[Sin[Pi 2^x]], {x, 0, k}, Assumptions -> {x \[Element] Reals && k \[Element] Reals}]

which evaluates to

and hence does not converge, i.e.

Limit[k/Sign[Sin[2^k \[Pi]]], k -> Infinity]

evaluates to

Interval[{-\[Infinity], \[Infinity]}]

So, I might have made a mistake after all. It is, however, weird that the Integral evaluates to something that is basically proportional to $k$. That does not appear to make sense. I must admit that the following baffles me a bit:

Evaluate[Integrate[Sign[Sin[Pi 2^x]], {x, 0, k}, Assumptions -> {x \[Element] Reals && k \[Element] Reals}]]
(*k/Sign[Sin[2^k \[Pi]]]*)

and

Table[Integrate[Sign[Sin[Pi 2^x]], {x, 0, k}], {k, 1, 4}]
(*{-1, -((2 (2 Log[2] - Log[3]))/Log[2]), (-11 Log[2] + 2 Log[5] + 
2 Log[7])/Log[2], -((2 (13 Log[2] - 2 Log[3] - Log[5] - Log[11] - Log[13]))/
Log[2])}*)

@Ilian Gachevski , @Vitaliy Kaurov , @Daniel Lichtblau : Am I using the assumptions wrong?

Cheers,

M

Thanks for all the help everyone!

I guess that this behaviour is documented:

It is one of these branch cut problems, I guess. Mathematica defines indefinite integrals of piecewise function up to constants at the discontinuities. It would be nice if somebody new an easy way of "removing" the discontinuities in these antiderivatives to get a continuous antiderivative.

Cheers,

Marco