Bedford's law relates to the distribution of leading digits in data. I was too lazy to reprogram David's program to look for leading digits, but I still wanted to see how well the digits in my codes correspond to Benford's law. I need to only look at digits in my code (instead of all characters, like David does) and then remove the zeros - as they are ignored as leading characters in Benford's law. Here's the result:
Show[DiscretePlot[
PDF[BenfordDistribution[10], x] // Evaluate, {x, 1, 9},
PlotMarkers -> Directive[Red, Automatic],
PlotRange -> {{1, 9}, {0, 0.35}}],
ListLinePlot[
ToExpression@
Sort@Select[
SortBy[{#[[1]],
N@#[[2]]/
Total[Select[
SortBy[{#[[1, 1]], Total[#[[;; , 2]]]} & /@
SplitBy[
Sort[Flatten[#[[2]] & /@ # & /@ data,
2]], #[[1]] &], #[[2]] &],
MemberQ[CharacterRange["1", "9"], #[[1]]] &][[All,
2]]]} & /@
Select[SortBy[{#[[1, 1]], Total[#[[;; , 2]]]} & /@
SplitBy[Sort[
Flatten[#[[2]] & /@ # & /@ data,
2]], #[[1]] &], #[[2]] &],
MemberQ[CharacterRange["1", "9"], #[[1]]] &], #[[2]] &],
MemberQ[CharacterRange["1", "9"], #[[1]]] &], PlotRange -> All]]
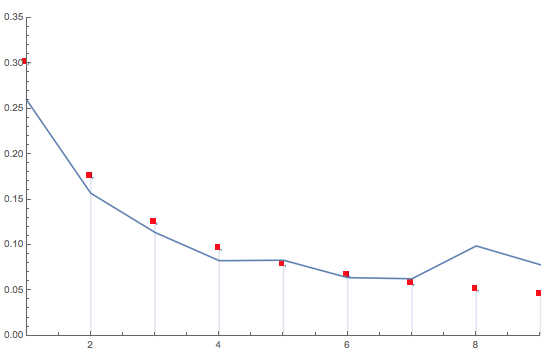
Of course, this data set does not really fit the Benford distribution:
datasymbols =
ConstantArray[#[[1]], Floor[#[[2]]]] & /@ (ToExpression@
Sort@Select[
SortBy[{#[[1]], N@#[[2]]} & /@
Select[SortBy[{#[[1, 1]], Total[#[[;; , 2]]]} & /@
SplitBy[
Sort[Flatten[#[[2]] & /@ # & /@ data,
2]], #[[1]] &], #[[2]] &],
MemberQ[CharacterRange["1", "9"], #[[1]]] &], #[[2]] &],
MemberQ[CharacterRange["1", "9"], #[[1]]] &]);
DistributionFitTest[RandomChoice[Flatten[datasymbols], 1000],
BenfordDistribution[10], "TestConclusion"]
which gives a rejection:
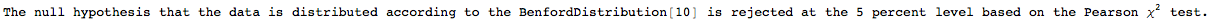
Ok, that is not really doing proper statistics on these numbers, but just playing a bit.
Cheers,
Marco