Marco Thank you, this is extremely helpful. Funny you mention over-sampled. You should see the original data, which is sampled 12 times even more frequently. This is telemetry data from a large machine, and high-frequency sampling is required to resolve certain mechanical responses, but certainly not thermal responses. The data example I supplied here is an example of a thermal response. Kindest regards,

Rich

Another thing is that the time series appears to be hopelessly oversampled. Everything becomes much faster if you first resample:

Show[ListLinePlot[MovingAverage[ArrayResample[testData, 2500], 50]], 
 ListPlot[FindPeaks[MovingAverage[ArrayResample[testData, 2500], 50], 25], PlotStyle -> Red]]

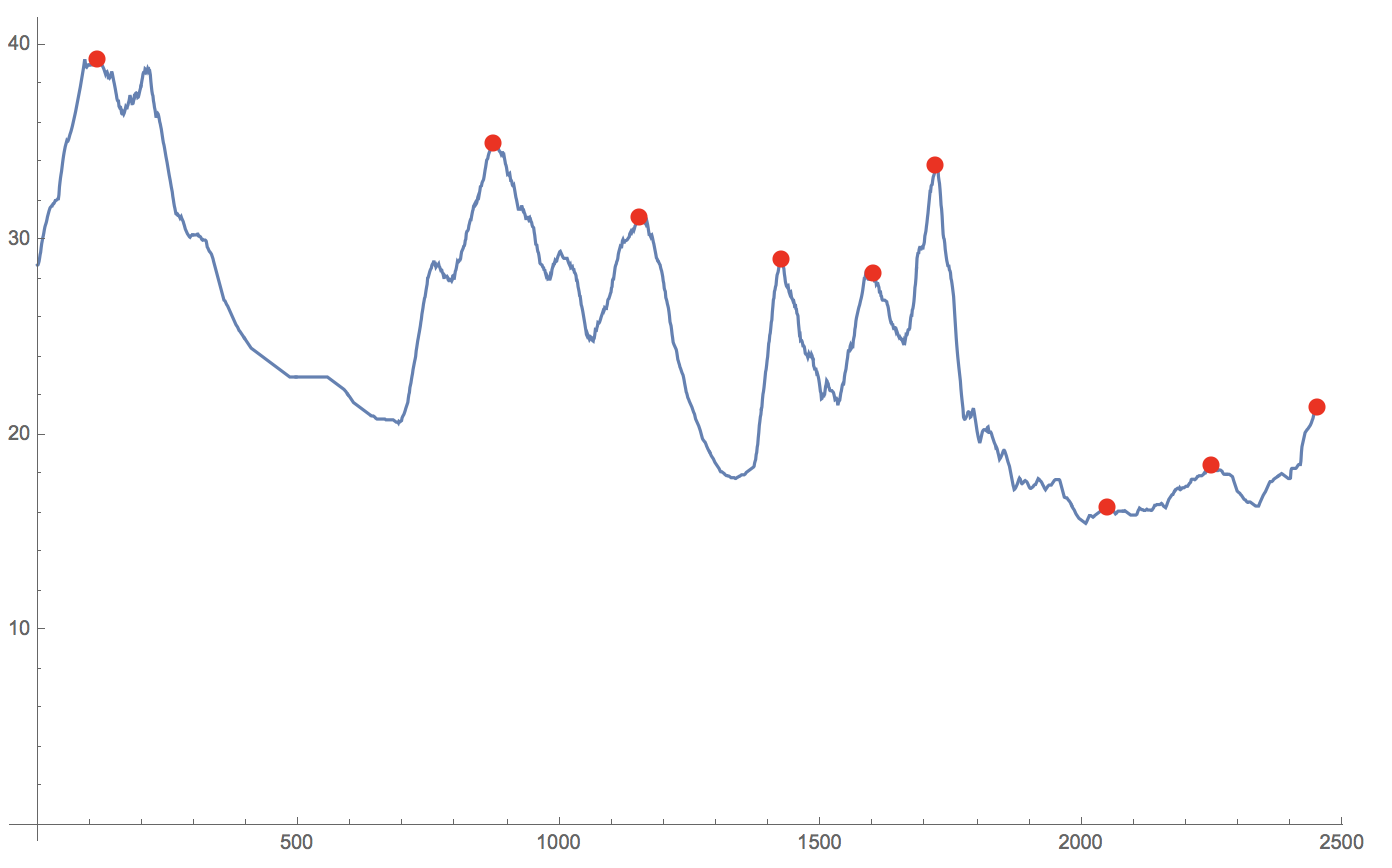
One can put a bit more effort (calculate window sizes in the resampled data) into this, but basically one can then also determine where the peaks are for the original sampling:

peaksresample = N /@ FindPeaks[MovingAverage[ArrayResample[testData, 2500], 50], 25];
{Length[testData]/2500.*#[[1]], #[[2]]} & /@ peaksresample

Cheers,

Marco

If you decimate the data (literally), and maybe use the first third of that, does the issue persist? If so, it would be with 100K elements, which might now be small enough to put into an attached notebook.

Hi Jos,

the way you calculate the peaks you get a result in the form {{index (!), value}, ...}. One possibility is to define your data as a time series and do it like so (compare with documentation on FindPeaks - under "Details and Options"):

ts = Transpose[test];
peaks = Normal@FindPeaks[TimeSeries[ts[[2]], {ts[[1]]}]]; 

Regards -- Henrik