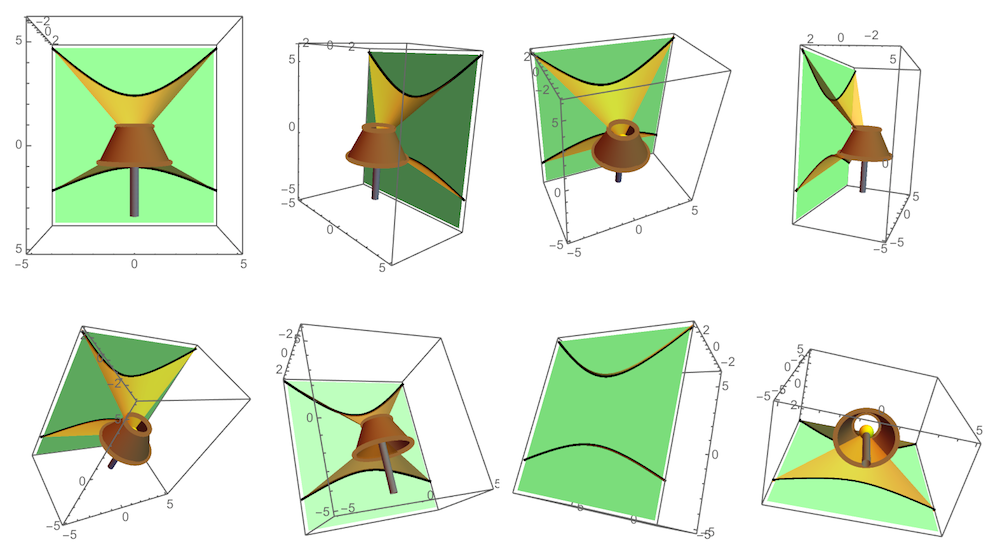
First, start with a lampshade that is a shaved off cone. In cylindrical coordinates, we can write the following equation:
shade[s_,t_]={(2-s/2) Cos[t],(2-s/2) Sin[t],s-1};
For this example, we can let $0\leq t<2 \pi$ and $0\leq s<2$. We also need a wall for the shadow to be cast upon:
wall[u_,v_]={u,3,v};
You can let u and v extend as far as necessary to make as large of a wall as you need. Finally, we need a lightbulb. Let's create a sphere of radius 1/2 centered at the origin:
sphere[s_,t_]=0.5{Cos[t] Sin[s],Sin[t] Sin[s],Cos[s]};
Finally, let's throw in a cylindrical base on the lamp with $0\leq t<2 \pi$ and $-4\leq s<-0.5$:
base[s_,t_]={.25 Cos[t],.25 Sin[t],s};
Here it is all plotted out, minus the shadow:
shadePlot=ParametricPlot3D[shade[s,t],{t,0,2Pi},{s,0,2},
PlotStyle->Brown,Mesh->False];
wallPlot=ParametricPlot3D[wall[u,v],{u,-5,5},{v,-5,6},
Mesh->False,PlotStyle->{Lighter[Lighter[Green]],Lighting->"Neutral",Specularity[0]}];
bulbPlot=ParametricPlot3D[sphere[s,t],{t,0,2Pi},{s,0,Pi},
PlotStyle->{Yellow},Mesh->False];
basePlot=ParametricPlot3D[{.25 Cos[t],.25 Sin[t],s},{s,-4,-.5},{t,0,2Pi},
PlotStyle->Gray,Mesh->False];
Show[shadePlot,wallPlot,bulbPlot,basePlot,PlotRange->{{-5,5},{-3,3},{-5,6}},
Background->White,Boxed->True,Axes->True]
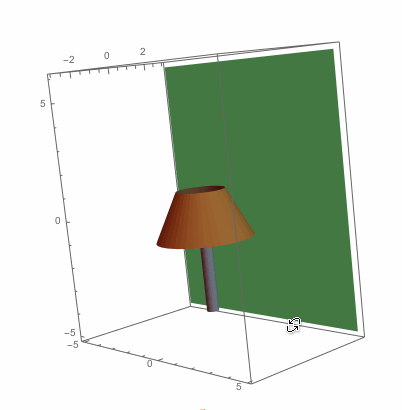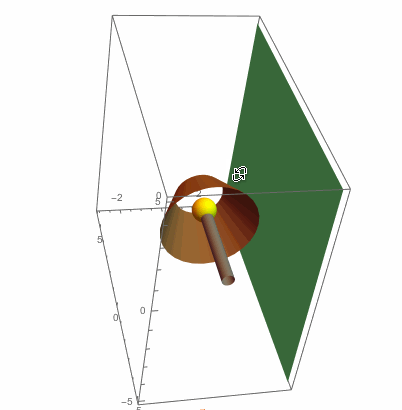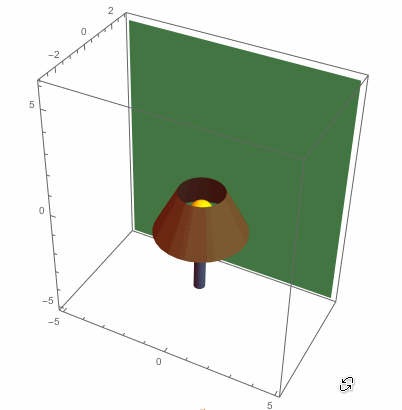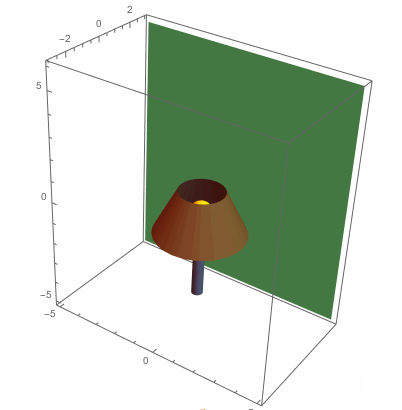
To figure out the shadow cast on the wall, we need to look at where a light ray from the light bulb hits the top edge of the lampshade. After this, we need to follow this light ray until it hits the wall. This will be the edge of the top shadow. First, we find the equation of the top of the lampshade:
topOfShade[t_]={Cos[t],Sin[t],1};
Next, we find the equation of a ray of light starting from the lightbulb, {0,0,0}, and hitting the top of the lampshade, {Cos[t],Sin[t],1}. This is just an equation for a line starting at the point {0,0,0} when s=0 and ending up at {Cos[t],Sin[t],1} when s=1:
topRay[s_,t_]={0,0,0}+s(topOfShade[t]-{0,0,0})
{s Cos[t], s Sin[t], s}
Note that this equation for a ray of light depends on the value of t we pick at the top of the lampshade. Next, we use Mathematica to find where this ray of light hits the wall. This is where the two equations, topRay[s,t] and wall[u,v] , have the same y-coordinate:
Solve[topRay[s,t][[2]]==wall[u,v][[2]],s]
{{s -> 3 Csc[t]}}
Finally, the equation of the shadow on the wall above the lampshade is given by evaluating topRay[s,t] at s = 3 Csc[t]:
topShadow[t_]=topRay[3 Csc[t],t]
{3 Cot[t], 3, 3 Csc[t]}
You can repeat this process for the bottom of the lampshade:
bottomOfShade[t_]={2Cos[t],2Sin[t],-1};
bottomRay[s_,t_]={0,0,0}+s(bottomOfShade[t]-{0,0,0});
Solve[bottomRay[s,t][[2]]==wall[u,v][[2]],s];
bottomShadow[t_]=bottomRay[3 Csc[t]/2,t]
{3 Cot[t], 3, -((3 Csc[t])/2)}
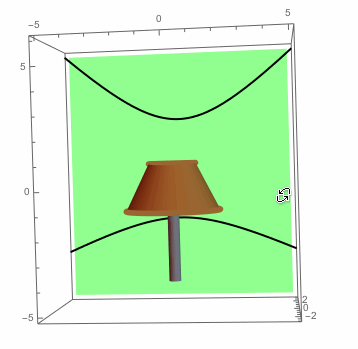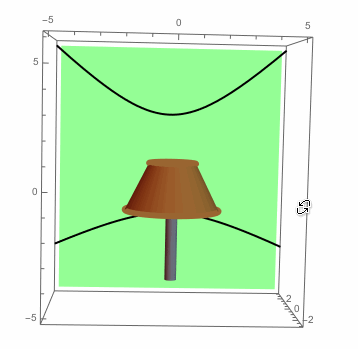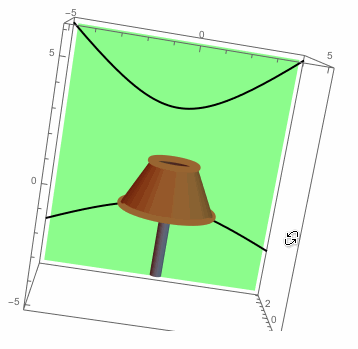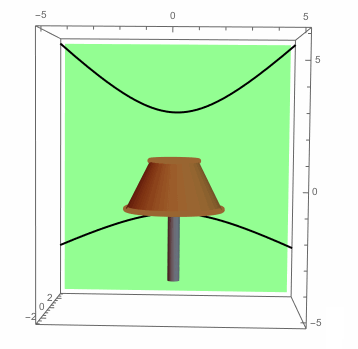
Here is the picture we started with, but with the shadows plotted on the wall:
shadePlot=ParametricPlot3D[{(2-s/2) Cos[t],(2-s/2) Sin[t],s-1},{t,0,2Pi},{s,0,2},
PlotStyle->Brown,Mesh->False];
basePlot=ParametricPlot3D[{.25 Cos[t],.25 Sin[t],s},{s,-4,-.5},{t,0,2Pi},
PlotStyle->Gray,Mesh->False];
topCirclePlot=ParametricPlot3D[{Cos[t],Sin[t],1},{t,0,2Pi},
PlotStyle->{Thickness[0.02],Brown}];
bottomCirclePlot=ParametricPlot3D[{2Cos[t],2Sin[t],-1},{t,0,2Pi},
PlotStyle->{Thickness[0.02],Brown}];
wallPlot=ParametricPlot3D[plane[u,v],{u,-5,5},{v,-5,6},
Mesh->False,PlotStyle->{Lighter[Lighter[Green]],Lighting->"Neutral",Specularity[0]}];
bulbPlot=ParametricPlot3D[{.5 Cos[t] Sin[s],.5 Sin[t] Sin[s],.5 Cos[s]},{t,0,2Pi},{s,0,Pi},
PlotStyle->{Yellow},Mesh->False];
topShadowPlot=ParametricPlot3D[topShadow[t],{t,0,Pi},PlotStyle->Black];
bottomShadowPlot=ParametricPlot3D[bottomShadow[t],{t,0,Pi},PlotStyle->Black];
Show[shadePlot,wallPlot,topCirclePlot,bottomCirclePlot,bulbPlot,topShadowPlot,bottomShadowPlot,
basePlot,PlotRange->{{-5,5},{-3,3},{-5,6}},Boxed->True,Axes->True,Background->White]
Now, you might ask what kind of curve
topShadow[t] = {3 Cot[t],3,3 Csc[t]}
is, and the same for
bottomShadow[t] = {3 Cot[t],3,-((3 Csc[t])/2)}
You can show pretty easily that these are hyperbolas. In general, say that you have an {x[t],y[t]} given by the following:
{x[t_],y[t_]}={a Cot[t],b Csc[t]};
Watch what happens when you compute $(y/b)^2-(x/a)^2$:
TrigReduce[(y[t]/b)^2-(x[t]/a)^2]
1
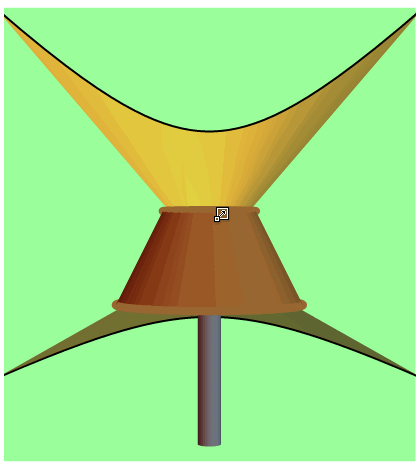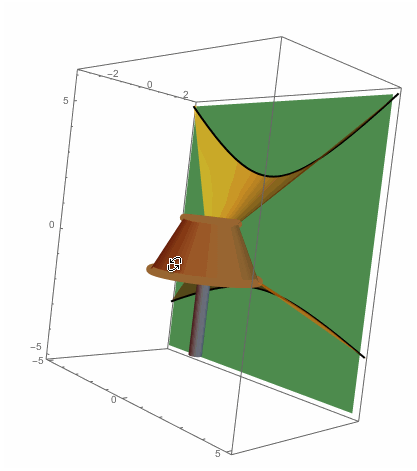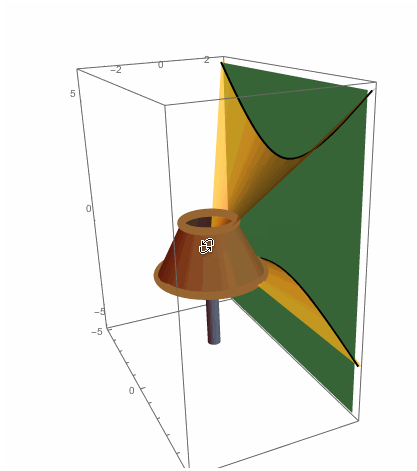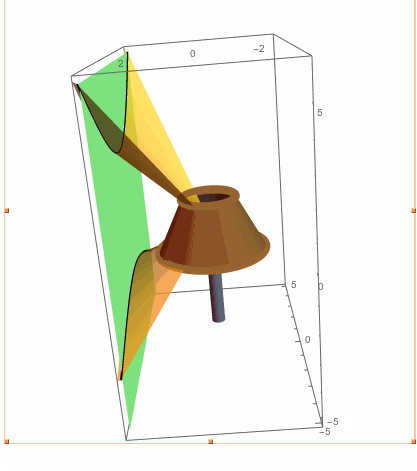
So it seems that our two shadows satisfy the equation $(y/b)^2-(x/a)^2=1$. That is, we have hyperbolic shadows. Finally, here's a rough picture of light rays escaping past the lampshade and creating our hyperbolic shadows:
shadePlot=ParametricPlot3D[{(2-s/2) Cos[t],(2-s/2) Sin[t],s-1},{t,0,2Pi},{s,0,2},
PlotStyle->Brown,Mesh->False];
basePlot=ParametricPlot3D[{.25 Cos[t],.25 Sin[t],s},{s,-4,-.5},{t,0,2Pi},
PlotStyle->Gray,Mesh->False];
topCirclePlot=ParametricPlot3D[{Cos[t],Sin[t],1},{t,0,2Pi},
PlotStyle->{Thickness[0.02],Brown}];
bottomCirclePlot=ParametricPlot3D[{2Cos[t],2Sin[t],-1},{t,0,2Pi},
PlotStyle->{Thickness[0.02],Brown}];
wallPlot=ParametricPlot3D[plane[u,v],{u,-5,5},{v,-5,6},
Mesh->False,PlotStyle->{Lighter[Lighter[Green]],Lighting->"Neutral",Specularity[0]}];
bulbPlot=ParametricPlot3D[{.5 Cos[t] Sin[s],.5 Sin[t] Sin[s],.5 Cos[s]},{t,0,2Pi},{s,0,Pi},
PlotStyle->{Yellow},Mesh->False];
topShadowPlot=ParametricPlot3D[topShadow[t],{t,0,Pi},PlotStyle->Black];
bottomShadowPlot=ParametricPlot3D[bottomShadow[t],{t,0,Pi},PlotStyle->Black];
topLightRaySurfacePlot=ParametricPlot3D[{0,0,0}-s (topShadow[t]-{0,0,0}),{t,Pi/6,5Pi/6},{s,-5,0},
Mesh->False,PlotStyle->Opacity[.7]];
bottomLightRaySurfacePlot=ParametricPlot3D[{0,0,0}-s (bottomShadow[t]-{0,0,0}),{t,Pi/6,5Pi/6},{s,-5,0},
Mesh->False,PlotStyle->Opacity[.7]];
Show[shadePlot,wallPlot,topCirclePlot,bottomCirclePlot,bulbPlot,topShadowPlot,
bottomShadowPlot,basePlot,topLightRaySurfacePlot,bottomLightRaySurfacePlot,
PlotRange->{{-5,5},{-3,3},{-5,6}},Boxed->True,Axes->True,Background->White]
 Attachments:
Attachments: