I have some Mathematica code that shows a behaviour I really cannot understand.
The code only contains a bunch of function definitions. If I paste it in the Notebook Front End and I evaluate it, I can then use those functions and they work as expected. Until here everything's fine.
The problems start when I try to create a Package with the same code. I exported the code from the Notebook to a Package and I saved to a file.m file. When I load the package with the command Get["path/to/file.m"], it is loaded correctly and the functions defined in the package become visible in the new Notebook where I loaded the package. The problem is that some functions (at the moment just one x2u) do not return the same results on evaluation if they are loaded from the package as if they were simply copy-pasted into the notebook.
I have read around several threads here, and also on stack exchange and in the documentation and I have already checked the following things in my code:
I know that when packages are loaded with Get[] only the initialization cell is evaluated. My Package is composed only by a single cell, which is also marked as Initialization Cell.
I know that Input Cells are discarded in Packages and only Code Cells are evaluated. The only cell in my Package is Code.
I know about $Context and $ContextPath and that some variables and functions defined in the Package can shadow globals. I am not sure I completely understood all the nuances of these concepts but I placed the function definitions in the private block of the package.
I also double-checked that the kernel was fresh in both cases:
- when I executed the code directly from the Notebook
- when I loaded the newly created package with the same code
After some work I managed to shrink the original Notebook to a minimal subset that reproduces the odd behaviour.
Here is the Notebook:
setenv[{e_Integer/;0<=e<=4,f_Integer/;0<=f<=11}]:=(
{esizesize,fsizesize}={e,f};
{esizemax,fsizemax}=
2^{e,f};
utagsize=1+f+e;
maxubits=1+esizemax+fsizemax+utagsize;
ubitmask=BitShiftLeft[1,utagsize-1];
fsizemask=(BitShiftLeft[1,f]-1);
esizemask=( ubitmask-1)-fsizemask;
efsizemask=BitOr[esizemask,fsizemask];
utagmask=BitOr[ ubitmask,efsizemask];
ulpu=BitShiftLeft[1,utagsize];
smallsubnormalu=efsizemask+ulpu;
smallnormalu=efsizemask+BitShiftLeft[1,maxubits-1-esizemax];
signbigu=BitShiftLeft[1,maxubits-1];
posinfu=signbigu-1- ubitmask;
maxrealu=posinfu-ulpu;
minrealu=maxrealu+signbigu;
neginfu=posinfu+signbigu;
negbigu=neginfu-ulpu;
qNaNu=posinfu+ ubitmask;
sNaNu=neginfu+ ubitmask;
negopeninfu=If[utagsize==1,2^^1101,BitShiftLeft[2^^1111,utagsize-1]];
posopeninfu=If[utagsize==1,2^^0101,BitShiftLeft[2^^0111,utagsize-1]];
negopenzerou=BitShiftLeft[2^^1001,utagsize-1];
maxreal=2^2^(esizemax-1) (2^fsizemax-1)/2^(fsizemax-1);
smallsubnormal=2^(2-2^(esizemax-1)-fsizemax);)
fsizeminus1[u_/;unumQ[u]]:=BitAnd[u,fsizemask]
fsize[u_/;unumQ[u]]:=1+fsizeminus1[u]
esizeminus1[u_/;unumQ[u]]:=BitShiftRight[BitAnd[u,esizemask],fsizesize]
esize[u_/;unumQ[u]]:=1+esizeminus1[u]
NaN=Indeterminate;
unumQ[x_]:=If[IntegerQ[x],If[x>=0\[And]x<=sNaNu,True,False],False]
floatQ[x_]:=If[NumericQ[x],If[Head[x]=!=Complex,True,False],If[x===\[Infinity]\[Or]x===-\[Infinity]\[Or]x===NaN,True,False]]
expovalue[u_/;unumQ[u]]:=expo[u]-bias[u]+1-hidden[u]
expomask[u_/;unumQ[u]]:=BitShiftLeft[BitShiftLeft[1,esize[u]]-1,fsize[u]+utagsize]
fracmask[u_/;unumQ[u]]:=BitShiftLeft[BitShiftLeft[1,fsize[u]]-1,utagsize]
bias[u_/;unumQ[u]]:=2^esizeminus1[u]-1
sign[u_/;unumQ[u]]:=Boole[BitAnd[u,signmask[u]]>0]
expo[u_/;unumQ[u]]:=BitShiftRight[BitAnd[u,expomask[u]],utagsize+fsize[u]]
hidden[u_/;unumQ[u]]:=Boole[expo[u]>0]
frac[u_/;unumQ[u]]:=BitShiftRight[BitAnd[u,fracmask[u]],utagsize]
exQ[u_/;unumQ[u]]:=BitAnd[ubitmask,u]==0
numbits[u_/;unumQ[u]]:=1+esize[u]+fsize[u]+utagsize
signmask[u_/;unumQ[u]]:=BitShiftLeft[1,numbits[u]-1]
scale[x_/;floatQ[x]\[And]x!=\[Infinity]\[And]x=!=NaN]:=If[x==0,0,\[LeftFloor]Log[2,Abs[x]]\[RightFloor]]
ne[x_/;floatQ[x]\[And]x!=\[Infinity]\[And]x=!=NaN]:=If[x==0\[Or]scale[x]==1,1,\[LeftCeiling]Log[2,1+Abs[scale[x]-1]]\[RightCeiling]+1]
x2u[x_/;floatQ[x]]:=Which[
x===NaN,qNaNu,
x==+\[Infinity],posinfu,
x==-\[Infinity],neginfu,
Abs[x]>maxreal,maxrealu+ubitmask+If[x<0,signbigu,0],
x==0,0,
Abs[x]<smallsubnormal,utagmask+If[x<0, signbigu,0],
Abs[x]<u2f[smallnormalu],
Module[{y},y=Abs[x]/smallsubnormal;
y=If[x<0, signbigu,0]+efsizemask+If[y!=\[LeftFloor]y\[RightFloor], ubitmask,0]+BitShiftLeft[\[LeftFloor]y\[RightFloor],utagsize];
While[BitAnd[BitShiftLeft[3,utagsize-1],y]==0,y=(y-BitAnd[efsizemask,y])/2+BitAnd[efsizemask,y]-1];y],
True,Module[{n=0,y,z},
y=Abs[x]/2^scale[x];n=0;While[\[LeftFloor]y\[RightFloor]!=y\[And]n<fsizemax,{n++,y*=2}];
If[y==\[LeftFloor]y\[RightFloor],y=n-Boole[n>0]
+BitShiftLeft[ne[x]-1,fsizesize]
+If[n==0,0,BitShiftLeft[\[LeftFloor]y\[RightFloor]-2^scale[y],utagsize]]
+BitShiftLeft[scale[x]+2^(ne[x]-1)-1,utagsize+n+Boole[n==0]]
+If[x<0,BitShiftLeft[1,utagsize+n+Boole[n==0]+ne[x]],0];
z=Log[2,1-Log[2,Abs[x]]];
If[IntegerQ[z]\[And]z>=0,BitShiftLeft[z,fsizesize]+ulpu+Boole[x<0]signmask[BitShiftLeft[z,fsizesize]],y],
(
z=\[LeftCeiling](Abs[x]/2^(scale[x]-fsizemax))\[RightCeiling]2^(scale[x]-fsizemax);n=Max[ne[x],ne[z]];
y=fsizemask
+BitShiftLeft[n-1,fsizesize]
+ ubitmask-ulpu
+BitShiftLeft[\[LeftFloor](z/2^scale[z]-1)2^fsizemax\[RightFloor],utagsize]
+BitShiftLeft[scale[z]+2^(n-1)-1,utagsize+fsizemax];
If[x<0,y+=signmask[y],y]
)]]]
u2f[u_/;unumQ[u]\[And]exQ[u]]:=Which[
u==posinfu,+\[Infinity],
u==neginfu,-\[Infinity],
True,(-1)^sign[u] 2^expovalue[u] (hidden[u]+frac[u]/2^fsize[u])]
If I evaluate it and then run following commands I get the following result which is correct. 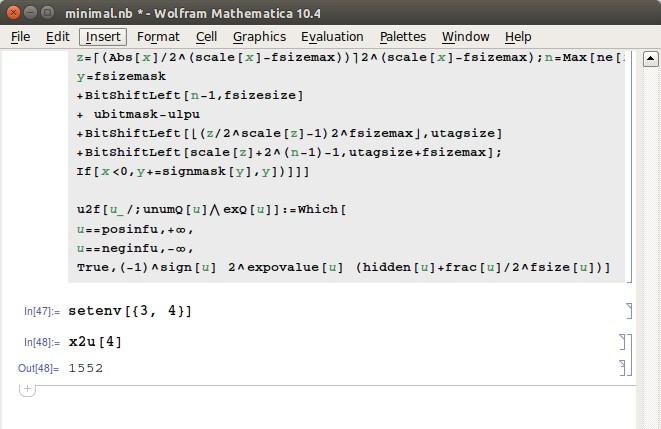
The code for the package instead is the following:
BeginPackage["minimal`"]
setenv::usage = "setenv[{esizesize, fsizesize}]"
x2u::usage = "x2u[float_number]"
Begin["`Private`"]
setenv[{e_Integer/;0<=e<=4,f_Integer/;0<=f<=11}]:=(
{esizesize,fsizesize}={e,f};
{esizemax,fsizemax}=
2^{e,f};
utagsize=1+f+e;
maxubits=1+esizemax+fsizemax+utagsize;
ubitmask=BitShiftLeft[1,utagsize-1];
fsizemask=(BitShiftLeft[1,f]-1);
esizemask=( ubitmask-1)-fsizemask;
efsizemask=BitOr[esizemask,fsizemask];
utagmask=BitOr[ubitmask,efsizemask];
ulpu=BitShiftLeft[1,utagsize];
smallsubnormalu=efsizemask+ulpu;
smallnormalu=efsizemask+BitShiftLeft[1,maxubits-1-esizemax];
signbigu=BitShiftLeft[1,maxubits-1];
posinfu=signbigu-1- ubitmask;
maxrealu=posinfu-ulpu;
minrealu=maxrealu+signbigu;
neginfu=posinfu+signbigu;
negbigu=neginfu-ulpu;
qNaNu=posinfu+ ubitmask;
sNaNu=neginfu+ ubitmask;
negopeninfu=If[utagsize==1,2^^1101,BitShiftLeft[2^^1111,utagsize-1]];
posopeninfu=If[utagsize==1,2^^0101,BitShiftLeft[2^^0111,utagsize-1]];
negopenzerou=BitShiftLeft[2^^1001,utagsize-1];
maxreal=2^2^(esizemax-1) (2^fsizemax-1)/2^(fsizemax-1);
smallsubnormal=2^(2-2^(esizemax-1)-fsizemax);)
fsizeminus1[u_/;unumQ[u]]:=BitAnd[u,fsizemask]
fsize[u_/;unumQ[u]]:=1+fsizeminus1[u]
esizeminus1[u_/;unumQ[u]]:=BitShiftRight[BitAnd[u,esizemask],fsizesize]
esize[u_/;unumQ[u]]:=1+esizeminus1[u]
NaN=Indeterminate;
unumQ[x_]:=If[IntegerQ[x],If[x>=0\[And]x<=sNaNu,True,False],False]
floatQ[x_]:=If[NumericQ[x],If[Head[x]=!=Complex,True,False],If[x===\[Infinity]\[Or]x===-\[Infinity]\[Or]x===NaN,True,False]]
expovalue[u_/;unumQ[u]]:=expo[u]-bias[u]+1-hidden[u]
expomask[u_/;unumQ[u]]:=BitShiftLeft[BitShiftLeft[1,esize[u]]-1,fsize[u]+utagsize]
fracmask[u_/;unumQ[u]]:=BitShiftLeft[BitShiftLeft[1,fsize[u]]-1,utagsize]
bias[u_/;unumQ[u]]:=2^esizeminus1[u]-1
sign[u_/;unumQ[u]]:=Boole[BitAnd[u,signmask[u]]>0]
expo[u_/;unumQ[u]]:=BitShiftRight[BitAnd[u,expomask[u]],utagsize+fsize[u]]
hidden[u_/;unumQ[u]]:=Boole[expo[u]>0]
frac[u_/;unumQ[u]]:=BitShiftRight[BitAnd[u,fracmask[u]],utagsize]
exQ[u_/;unumQ[u]]:=BitAnd[ubitmask,u]==0
numbits[u_/;unumQ[u]]:=1+esize[u]+fsize[u]+utagsize
signmask[u_/;unumQ[u]]:=BitShiftLeft[1,numbits[u]-1]
u2f[u_/;unumQ[u]\[And]exQ[u]]:=Which[
u==posinfu,+\[Infinity],
u==neginfu,-\[Infinity],
True,(-1)^sign[u] 2^expovalue[u] (hidden[u]+frac[u]/2^fsize[u])]
scale[x_/;floatQ[x]\[And]x!=\[Infinity]\[And]x=!=NaN]:=If[x==0,0,\[LeftFloor]Log[2,Abs[x]]\[RightFloor]]
ne[x_/;floatQ[x]\[And]x!=\[Infinity]\[And]x=!=NaN]:=If[x==0\[Or]scale[x]==1,1,\[LeftCeiling]Log[2,1+Abs[scale[x]-1]]\[RightCeiling]+1]
x2u[x_/;floatQ[x]]:=Which[
x===NaN,qNaNu,
x==+\[Infinity],posinfu,
x==-\[Infinity],neginfu,
Abs[x]>maxreal,maxrealu+ubitmask+If[x<0,signbigu,0],
x==0,0,
Abs[x]<smallsubnormal,utagmask+If[x<0, signbigu,0],
Abs[x]<u2f[smallnormalu],
Module[{y},y=Abs[x]/smallsubnormal;
y=If[x<0, signbigu,0]+efsizemask+If[y!=\[LeftFloor]y\[RightFloor], ubitmask,0]+BitShiftLeft[\[LeftFloor]y\[RightFloor],utagsize];
While[BitAnd[BitShiftLeft[3,utagsize-1],y]==0,y=(y-BitAnd[efsizemask,y])/2+BitAnd[efsizemask,y]-1];y],
True,Module[{n=0,y,z},
y=Abs[x]/2^scale[x];n=0;While[\[LeftFloor]y\[RightFloor]!=y\[And]n<fsizemax,{n++,y*=2}];
If[y==\[LeftFloor]y\[RightFloor],y=n-Boole[n>0]
+BitShiftLeft[ne[x]-1,fsizesize]
+If[n==0,0,BitShiftLeft[\[LeftFloor]y\[RightFloor]-2^scale[y],utagsize]]
+BitShiftLeft[scale[x]+2^(ne[x]-1)-1,utagsize+n+Boole[n==0]]
+If[x<0,BitShiftLeft[1,utagsize+n+Boole[n==0]+ne[x]],0];
z=Log[2,1-Log[2,Abs[x]]];
If[IntegerQ[z]\[And]z>=0,BitShiftLeft[z,fsizesize]+ulpu+Boole[x<0]signmask[BitShiftLeft[z,fsizesize]],y],
(
z=\[LeftCeiling](Abs[x]/2^(scale[x]-fsizemax))\[RightCeiling]2^(scale[x]-fsizemax);n=Max[ne[x],ne[z]];
y=fsizemask
+BitShiftLeft[n-1,fsizesize]
+ ubitmask-ulpu
+BitShiftLeft[\[LeftFloor](z/2^scale[z]-1)2^fsizemax\[RightFloor],utagsize]
+BitShiftLeft[scale[z]+2^(n-1)-1,utagsize+fsizemax];
If[x<0,y+=signmask[y],y]
)]]]
End[]
EndPackage[]
If I close Mathematica and reopen it (so that I am sure I have a fresh Kernel), and I try to Get[] the package and run the same commands as above I get the following wrong result. 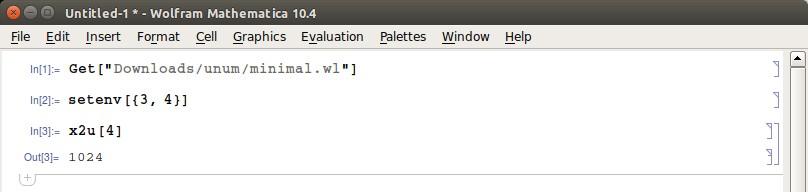
What am I doing wrong?
Unfortunately the minimal example is not so minimal, but I didn't write the original code myself. It comes from a Notebook I got from the internet. It's a Notebook freely distributed with this book: http://crcpress.com/The-End-of-Error-Unum-Computing/Gustafson/p/book/9781482239867 You can find it in a .zip file in the Downloads/Updates tab, on the left, just below the picture of the book cover. In the original Notebook there is a ton of code, but the part I provided should be enough and self-contained and I have not been able to reduce it further. I also tried with some code I wrote, but I have not been able to obtain the same misbehaviour.
As you can see the code in the Notebook and in the Package are really the same, except for the BeginPackage[] EndPackage[] portions.