I came across Laplace Interpolation as a specialized interpolation method for restoring missing data on a grid and was so delighted by the results that I thought it might be worth sharing. (see e.g. here: http://numerical.recipes/CS395T/lectures2010/201019LaplaceInterpolation.pdf)
So the basic idea of Laplace interpolation is to set $y(x_i)=y_i$ at every known data point and solve $\nabla^2 y=0$ at every unknown point.
Before I show the code let's take a look at the results. The following shows, the original image (left), the damaged image with 40% healthy pixels (middle) and the repaired image (right).
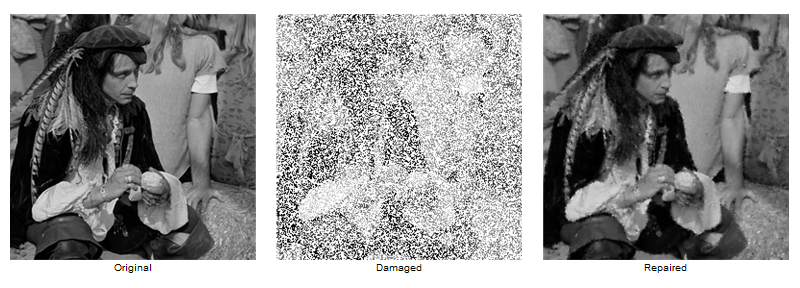
The Laplace Interpolation
Each pixel gives one equation. Consider an arbitrary pixel $y_0$. Its value is determined by the neighborhood:

To compute $y_0$
If the pixel is ok:
$$y_0=y_{0,measured}$$
If the pixel is damaged;
$$y_0-\frac{1}{4}y_u-\frac{1}{4}y_d-\frac{1}{4}y_l-\frac{1}{4}y_r=0$$
and the following special cases (boundary):
(left and right boundary)
$$y_0-\frac{1}{2}y_u-\frac{1}{2}y_d=0$$
(top and bottom boundary)
$$y_0-\frac{1}{2}y_l-\frac{1}{2}y_r=0$$
(top left corner)
$$y_0-\frac{1}{2}y_r-\frac{1}{2}y_d=0$$
(top right corner)
$$y_0-\frac{1}{2}y_l-\frac{1}{2}y_d=0$$ (bottom left corner)
$$y_0-\frac{1}{2}y_r--\frac{1}{2}y_u=0$$
(bottom right corner)
$$y_0-\frac{1}{2}y_l-\frac{1}{2}y_u=0$$ There is exactly one equation for each grid point, so we can solve this as a giant (sparse!) linear system,
The Algorithm
I decided to flatten the image into a 1-D list enumerating as shown here: 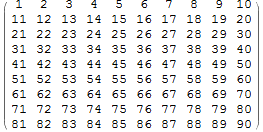
Taking this scheme I set up the test functions to decide whether a given index belongs to the image edges or corners;
topLeftCornerQ[index_Integer,{xdim_Integer,ydim_Integer}]:=index==1
topRightCornerQ[index_Integer,{xdim_Integer,ydim_Integer}]:=index==xdim
bottomRightCornerQ[index_Integer,{xdim_Integer,ydim_Integer}]:=(index==(xdim*ydim))
bottomLeftCornerQ[index_Integer,{xdim_Integer,ydim_Integer}]:=(index==xdim*(ydim-1)+1)
leftEdgeQ[index_Integer,{xdim_Integer,ydim_Integer}]:=(Mod[index,xdim]-1==0)&&Not[bottomLeftCornerQ[index,{xdim,ydim}]]&&Not[topLeftCornerQ[index,{xdim,ydim}]]
rightEdgeQ[index_Integer,{xdim_Integer,ydim_Integer}]:=(Mod[index,xdim]==0)&&Not[bottomRightCornerQ[index,{xdim,ydim}]]&&Not[topRightCornerQ[index,{xdim,ydim}]]
topEdgeQ[index_Integer,{xdim_Integer,ydim_Integer}]:=(2<= index<=xdim-1)
bottomEdgeQ[index_Integer,{xdim_Integer,ydim_Integer}]:=(xdim*(ydim-1)+2<= index<=xdim*ydim-1)
We then need some functions to select the boundary values:
yLeft[index_,{xdim_,ydim_}]:=Module[{pos},
Which[
leftEdgeQ[index,{xdim ,ydim }],{},
topLeftCornerQ[index,{xdim ,ydim }],{},
bottomLeftCornerQ[index,{xdim ,ydim }],{},
True,index-1
]
]
yRight[index_,{xdim_,ydim_}]:=Module[{pos},
Which[
rightEdgeQ[index,{xdim ,ydim }],{},
topRightCornerQ[index,{xdim ,ydim }],{},
bottomRightCornerQ[index,{xdim ,ydim }],{},
True,index+1
]
]
yDown[index_,{xdim_,ydim_}]:=Module[{pos},
Which[
bottomEdgeQ[index,{xdim ,ydim }],{},
bottomLeftCornerQ[index,{xdim ,ydim }],{},
bottomRightCornerQ[index,{xdim ,ydim }],{},
True,index+xdim
]
]
yUp[index_,{xdim_,ydim_}]:=Module[{pos},
Which[
topEdgeQ[index,{xdim ,ydim }],{},
topLeftCornerQ[index,{xdim ,ydim }],{},
topRightCornerQ[index,{xdim ,ydim }],{},
True,index-xdim
]
]
(The sanity checks inside can also be removed).
The input to the interpolation is an array where the damaged pixel are indicated by their value $10^{99}$ Every instance of $10^{99}$ is replaced by a enumerated variable $y_i$, where $i$ is the pixel index.
{xdim , ydim} = Dimensions[array];
arrayList = Flatten[array, 1];
symbolList = ParallelTable[ToExpression["y" <> ToString[i]], {i, 1, xdim*ydim}];
(*replace unknown pixel with y-variable*)
yList = MapIndexed[If[#1 == 10^99, symbolList[[First[#2]]], #1] &,arrayList];
With yListwe can now construct the list of equations to solve:
createEquations[yList_, {xdim_, ydim_}] := Module[{value},
DeleteCases[ParallelTable[
value = yList[[i]];
Which[
NumberQ[value], {},
topLeftCornerQ[i, {xdim, ydim}], value - 0.5 yList[[yRight[i, {xdim, ydim}]]] - 0.5 yList[[yDown[i, {xdim, ydim}]]] == 0.,
topRightCornerQ[i, {xdim, ydim}], value - 0.5 yList[[yLeft[i, {xdim, ydim}]]] - 0.5 yList[[yDown[i, {xdim, ydim}]]] == 0.,
bottomLeftCornerQ[i, {xdim, ydim}], value - 0.5 yList[[yRight[i, {xdim, ydim}]]] - 0.5 yList[[yUp[i, {xdim, ydim}]]] == 0.,
bottomRightCornerQ[i, {xdim, ydim}], value - 0.5 yList[[yLeft[i, {xdim, ydim}]]] - 0.5 yList[[yUp[i, {xdim, ydim}]]] == 0.,
leftEdgeQ[i, {xdim, ydim}], value - 0.5 yList[[yDown[i, {xdim, ydim}]]] - 0.5 yList[[yUp[i, {xdim, ydim}]]] == 0.,
rightEdgeQ[i, {xdim, ydim}], value - 0.5 yList[[yDown[i, {xdim, ydim}]]] - 0.5 yList[[yUp[i, {xdim, ydim}]]] == 0.,
topEdgeQ[i, {xdim, ydim}], value - 0.5 yList[[yLeft[i, {xdim, ydim}]]] - 0.5 yList[[yRight[i, {xdim, ydim}]]] == 0.,
bottomEdgeQ[i, {xdim, ydim}], value - 0.5 yList[[yLeft[i, {xdim, ydim}]]] - 0.5 yList[[yRight[i, {xdim, ydim}]]] == 0.,
True, value - 0.25 yList[[yLeft[i, {xdim, ydim}]]] - 0.25 yList[[yRight[i, {xdim, ydim}]]] - 0.25 yList[[yUp[i, {xdim, ydim}]]] - 0.25 yList[[yDown[i, {xdim, ydim}]]]], {i, 1,
Length[yList]}], {}]]
Putting it all together and adding the LinearSolver as well as reformate the output array:
laplaceInterpolate[array_] :=
Module[{xdim , ydim , list, yList, symbolList, arrayList, unknowns,
equations, coeffArrays, rhs, m, sol, repl},
{xdim , ydim} = Dimensions[array];
arrayList = Flatten[array, 1];
symbolList =
ParallelTable[ToExpression["y" <> ToString[i]], {i, 1, xdim*ydim}];
(*replace unknown pixel with y-variable*)
yList =
MapIndexed[If[#1 == 10^99, symbolList[[First[#2]]], #1] &,
arrayList];
unknowns = DeleteCases[yList, _?NumberQ];
equations = createEquations[yList, {xdim , ydim}];
(*Print[Row[{Length[unknowns],": damaged pixel, ",Length[
equations],": equations"}]];*)
{rhs, m} = CoefficientArrays[equations, unknowns];
sol = Abs@LinearSolve[m, rhs];
repl = Thread[unknowns -> sol];
Partition[yList /. repl, xdim]
]
Let's add some convenience functions:
damageImage[im_Image, healthyPixel_Integer] :=
Module[{imDat, xdim, ydim, black, points, bad},
imDat = ImageData[im];
bad = If[ImageChannels[im] == 3, {10^99, 10^99, 10^99}, 10^99];
{xdim, ydim} = ImageDimensions[im];
black = ConstantArray[bad, {xdim, ydim}];
points =
RandomSample[Flatten[Table[{i, j}, {i, 1, xdim}, {j, 1, ydim}], 1],
healthyPixel];
Table[black[[points[[i, 1]], points[[i, 2]]]] =
imDat[[points[[i, 1]], points[[i, 2]]]], {i, 1, Length[points]}];
black]
repairImage[im_Image] := Module[{repaired, channels},
If[ImageChannels[im] == 1,
repaired = Image@laplaceInterpolate[ImageData[im]],
channels = ImageData /@ ColorSeparate[im];
repaired =
ColorCombine[Image /@ (laplaceInterpolate[#] & /@ channels),
"RGB"]];
repaired]
Action
We can now test the procedure. The function damageImage takes an input image and keeps healthyPixel random pixel positions and destroys all other image pixel. I resize the image to 128x128 to keep the computing times low. Any performance improvements are appreciated.
im = ImageResize[ExampleData[{"TestImage", "Man"}], {128}];
dam = Image@damageImage[im, Round[0.9 128*128]];
rep = repairImage[dam];
GraphicsRow[{
Labeled[Image[im, ImageSize -> 250], "Original", ImageMargins -> 10],
Labeled[Image[dam, ImageSize -> 250], "Damaged (10%)", ImageMargins -> 10],
Labeled[Image[rep, ImageSize -> 250], "Repaired", ImageMargins -> 10]}, ImageSize -> 800, Spacings -> 0]]

It is amazing how much information can be restored:
im = ImageResize[ExampleData[{"TestImage", "Man"}], {128}];
dam = Image@damageImage[im, Round[0.1 128*128]];
rep = repairImage[dam];
GraphicsRow[{
Labeled[Image[im, ImageSize -> 250], "Original", ImageMargins -> 10],
Labeled[Image[dam, ImageSize -> 250], "Damaged (90%)",ImageMargins -> 10],
Labeled[Image[rep, ImageSize -> 250], "Repaired", ImageMargins -> 10]}, ImageSize -> 800, Spacings -> 0]
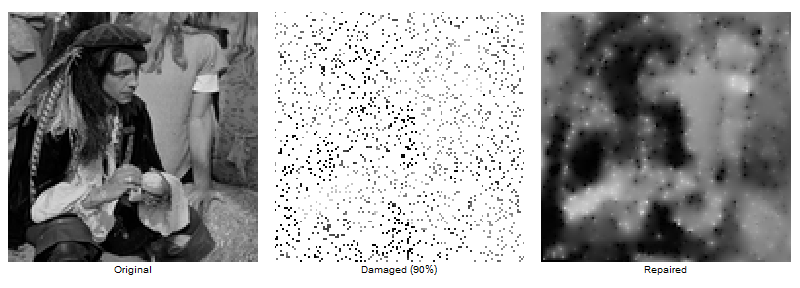
In case of an RGB image each channel has to be interpolated seperately.
im = ImageResize[ExampleData[{"TestImage", "Lena"}], {128}];
dam = Image@damageImage[im, Round[0.25 128*128]];
rep = repairImage[dam];
GraphicsRow[{
Labeled[Image[im, ImageSize -> 250], "Original", ImageMargins -> 10],
Labeled[Image[dam, ImageSize -> 250], "Damaged (75%)", ImageMargins -> 10],
Labeled[Image[rep, ImageSize -> 250], "Repaired", ImageMargins -> 10]}, ImageSize -> 800, Spacings -> 0]
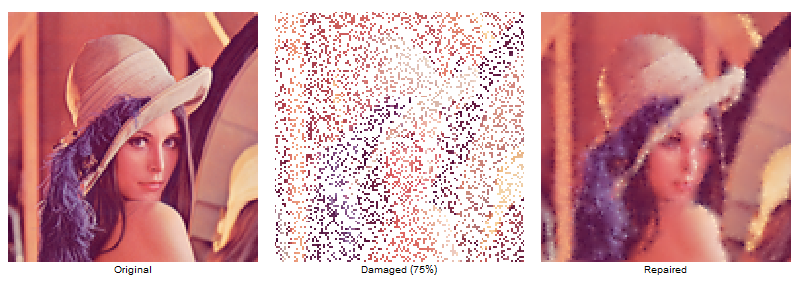
 Attachments:
Attachments: