Mathematica can do it with ComplexExpand:

Sum[Simplify@
  ComplexExpand@Abs[Exp[2 Pi I k/n] - Exp[2 Pi I (k - 1)/n]], {k, n}]
Limit[%, n -> Infinity]

By default Limit takes the limit from the right. The option Direction is there for us to choose the direction: -1 is for the limit from the right (in the negative direction) and 1 for the limit from the left (in the positive direction):

Limit[(Log[1 - x] - Sin[x])/(1 - Cos[x]^2), x -> 0, Direction -> 1]
Limit[(Log[1 - x] - Sin[x])/(1 - Cos[x]^2), x -> 0, Direction -> -1]

It's no a Bug. It's seems a Simplify with helps ComplexExpand command simplifies and solves this problem.

It is a DirectedInfinity. Your function is going to infinity in the complex plane along that direction. Check out the plot:

ParametricPlot[
 ReIm[((15 + 2 x)^(1/3) + 1)/((9 + x)^(1/3) + x + 7)], {x, -8, -7.5}, 
 AxesOrigin -> {0, 0}, 
 Epilog -> {Dashed, HalfLine[{0, 0}, ReIm[(1 + (-1)^(1/3))/Sqrt[3]]]}]

Thank you, Mariusz?

Another limit, the same difficulty...

In the following example I intentionally gives the result at the beginning because it's not difficult to solve the problem analytically.

So, I tried to verify In Mathematica the result of this example

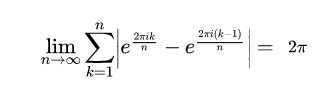
The Mathematica gives

In[1]:= Limit[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(2.  \[Pi]\ I\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2  \[Pi]\ I\ \((k - 1)\)\), \(n\)]]]\)\), 
 n -> \[Infinity]]

Out[1]= Limit[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(\((0.`  + 6.283185307179586`\ I)\)\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2\ I\ \((\(-1\) + k)\)\ \[Pi]\), \(n\)]]]\)\), 
 n -> \[Infinity]]

It's interesting that when I tried to compute simply the numerical evaluations of the expression under the limit, I obtained

In[2]:= Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(2.  \[Pi]\ I\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2  \[Pi]\ I\ \((k - 1)\)\), \(n\)]]]\)\), {n, 10000, 
10010}]

Out[2]= {6.28319, 6.28319, 6.28319, 6.28319, 6.28319, 6.28319, \
6.28319, 6.28319, 6.28319, 6.28319, 6.28319}

In[3]:= Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(2.  \[Pi]\ I\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2  \[Pi]\ I\ \((k - 1)\)\), \(n\)]]]\)\), {n, 100000, 
100010}]

Out[3]= {6.28319, 6.28319, 6.28319, 6.28319, 6.28319, 6.28319, \
6.28319, 6.28319, 6.28319, 6.28319, 6.28319}

These results are approximately equal to $2\pi$. Why didn't work the function Limit[]?

Thank you, Gianluca, for a simple and clear answer to the question!

Another strange result for the Limit function:

Limit[(Power[15 + 2 x, (3)^-1] + 1)/(Power[9 + x, (3)^-1] + x + 7), 
 x -> -8]

How to understand it?

btw L'Hopital rule is flawed i hope your not using that to determine if Mathematica is correct

your comparing points on two function lines, but l'hopital tries a trick using one line, the data isn't always there: L'Hopital's rules is plain wrong - wrong but easy!

To add to the remark by @GianlucaGorni, l'Hopital's rule gives the correct result here.

D[(CubeRoot[15 + 2 x] + 1), x]/D[CubeRoot[9 + x] + x + 7, x] /. x -> -8

(* Out[960]= 1/2 *)

This also raises a question: What exactly is "wrong" with l'Hopital's rule? (There is some literature on this, by the way.)