It's NOT a error, because from Mathematica Documentation Center:

By default Limit takes the limit from the right. The option Direction is there for us to choose the direction: -1 is for the limit from the right (in the negative direction) and 1 for the limit from the left (in the positive direction):

Limit[(Log[1 - x] - Sin[x])/(1 - Cos[x]^2), x -> 0, Direction -> 1]
Limit[(Log[1 - x] - Sin[x])/(1 - Cos[x]^2), x -> 0, Direction -> -1]

Another limit, the same difficulty...

In the following example I intentionally gives the result at the beginning because it's not difficult to solve the problem analytically.

So, I tried to verify In Mathematica the result of this example

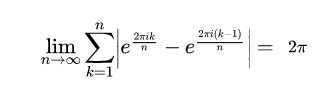
The Mathematica gives

In[1]:= Limit[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(2.  \[Pi]\ I\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2  \[Pi]\ I\ \((k - 1)\)\), \(n\)]]]\)\), 
 n -> \[Infinity]]

Out[1]= Limit[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(\((0.`  + 6.283185307179586`\ I)\)\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2\ I\ \((\(-1\) + k)\)\ \[Pi]\), \(n\)]]]\)\), 
 n -> \[Infinity]]

It's interesting that when I tried to compute simply the numerical evaluations of the expression under the limit, I obtained

In[2]:= Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(2.  \[Pi]\ I\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2  \[Pi]\ I\ \((k - 1)\)\), \(n\)]]]\)\), {n, 10000, 
10010}]

Out[2]= {6.28319, 6.28319, 6.28319, 6.28319, 6.28319, 6.28319, \
6.28319, 6.28319, 6.28319, 6.28319, 6.28319}

In[3]:= Table[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 1\), \(n\)]\(Abs[
\*SuperscriptBox[\(E\), 
FractionBox[\(2.  \[Pi]\ I\ k\), \(n\)]] - 
\*SuperscriptBox[\(E\), 
FractionBox[\(2  \[Pi]\ I\ \((k - 1)\)\), \(n\)]]]\)\), {n, 100000, 
100010}]

Out[3]= {6.28319, 6.28319, 6.28319, 6.28319, 6.28319, 6.28319, \
6.28319, 6.28319, 6.28319, 6.28319, 6.28319}

These results are approximately equal to $2\pi$. Why didn't work the function Limit[]?

Thank you, Mariusz. Is this a bug? Must we report it to WRI?

Thank you, Gianluca, for a simple and clear answer to the question!

Agree!

Basically it blows up to 'an infinity'; not negative infinity, not positive infinite, or i*infinity, but roughly (0.866025 + 0.5 I) * infinity ....

Check the FullForm of your expression to better understand it perhaps...

Bingo! Finally, I solved it after clarifying that Mathematica has two different cube roots for Power[ ] function and Surd[ ] function. In the above example, It must be used Surd[ ] function. So:

In[1]:= Limit[(Surd[15 + 2 x, 3] + 1)/(Surd[9 + x, 3] + x + 7), 
 x -> -8]

Out[1]= 1/2

The task was to compute directly the limit with the Mma standard function. So, we found that Surd[] is more appropriate in this case that Power[].

Or, we can use CubeRoot[]:

In[1]:= Limit[(CubeRoot[15 + 2 x] + 1)/(CubeRoot[9 + x] + x + 7), 
 x -> -8]

Out[1]= 1/2

To add to the remark by @GianlucaGorni, l'Hopital's rule gives the correct result here.

D[(CubeRoot[15 + 2 x] + 1), x]/D[CubeRoot[9 + x] + x + 7, x] /. x -> -8

(* Out[960]= 1/2 *)

This also raises a question: What exactly is "wrong" with l'Hopital's rule? (There is some literature on this, by the way.)

Yes, if you don't care about the precise conditions, you find "counterexamples". The "counterexample" in the paper is very interesting, but it relies on infinitely many oscillations and algebraic cancellation, a combination that is unlikely to happen in the wild. I would say that with L'Hopital's rule you can most safely get away with ignoring the condition that the denominator be monotonic, unless somebody willfully laid a trap for you.