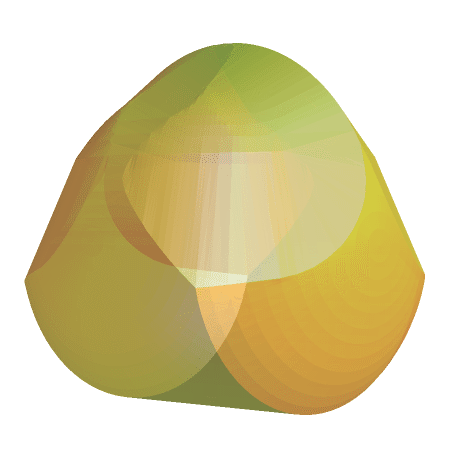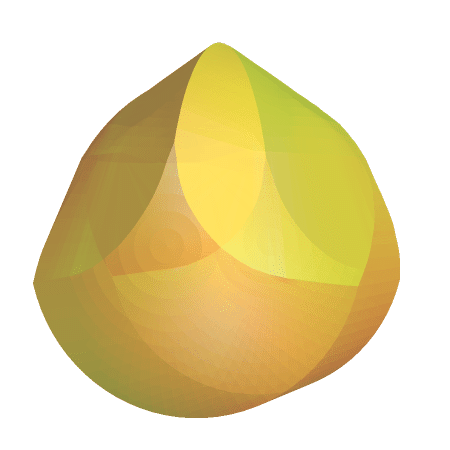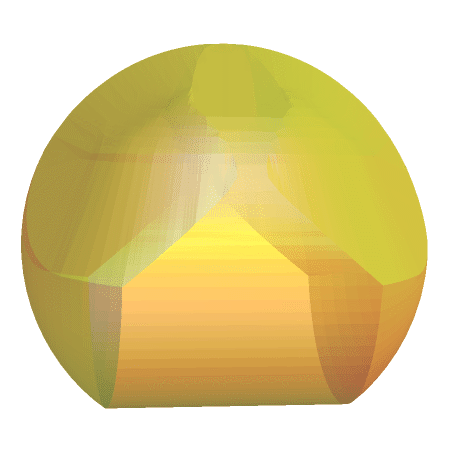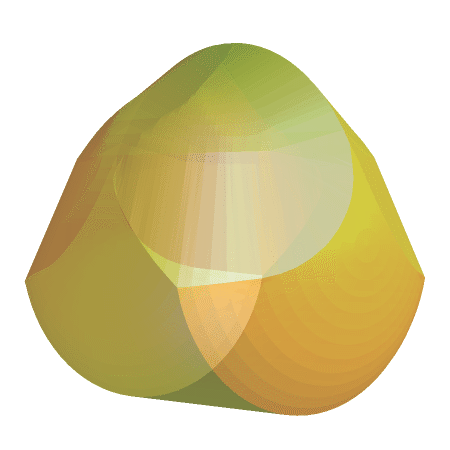This is an excellent question! First, a little bit of history from
this Wikipedia article.
A gömböc or gomboc is a convex three-dimensional homogeneous body which, when resting on a flat surface, has just one stable and one unstable point of equilibrium. Its existence was conjectured by Russian mathematician Vladimir Arnold in 1995 and proven in 2006 by Hungarian scientists Gábor Domokos and Péter Várkonyi.
The gömböc shape is not unique; it has countless varieties, most of which are very close to a sphere and all have very strict shape tolerance (about 0.1 mm per 10 cm). The most famous solution has a sharpened top and helped to explain the body structure of some turtles in relation to their ability to return to equilibrium position after being placed upside down. ...The rigorous proof of the solution can be found in
references of their work. The summary of the results is that the three-dimensional homogeneous convex (mono-monostatic) body, which has one stable and one unstable equilibrium point, does exist and is not unique.
Such bodies are hard to visualize, describe or identify. ... Domokos and his wife developed a classification system for shapes based on their points of equilibrium by analyzing pebbles and noting their equilibrium points. In one experiment, they tried 2000 pebbles collected at the beaches of the Greek island of Rhodes and found no single mono-monostatic body among them, illustrating the difficulty to find or construct such a body. ~ Wikipedia
Basically what it means is that there is no analytic description. As far as I know the most famous mono-monostatic gömböc (that reminiscent of turtles) was built by trail and error method using
3D printing technology. A few thoughts immediately come to mind:
- If there is a large space of shapes that are hard to find, perhaps NKS computational methods can be developed for searching that space
- This type of shapes is rather more than fun to 3D print
Well, luckily for us MakerBots Thingiverse has a
submission of a shape that the author was able to get by reverse engineering. One can impor that .STL file into Mathemtica with a single line:
Import["http://kaurov.com/TMP/gomboc-reverse-engineered.stl"]

But it would be rather cool to get the descriptive geometry and make a better visualization -
it is large, wait till 2nd image loads below the code.
obj = Import["http://kaurov.com/TMP/gomboc-reverse-engineered.stl", "PolygonObjects"];
gomboc = Graphics3D[{FaceForm[
Directive[Specularity[White, 20], Yellow, Opacity[.5]]],
EdgeForm[], obj}, Boxed -> False];
frames = Table[Show[gomboc,
ViewPoint -> RotationTransform[t, {0, 1, 0}][{3, 0, 3}],
ViewVertical -> {0, -1, 0}, SphericalRegion -> True,
ViewAngle -> .25, ImageSize -> 500], {t, 0, 2 Pi, .1}];
Export["gomboc.gif", frames]