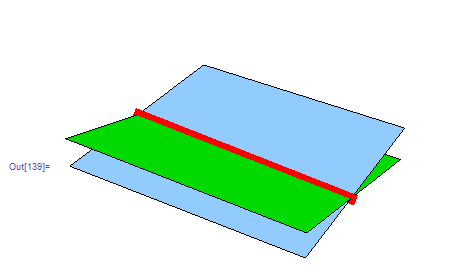
No need for a point. Use parameteric representation
ClearAll[x, y, z, t];
p1 = x + 5 y + 2 z + 3 == 0; (*equation of first plane*)
p2 = 2 x + 3 y + 6 z + 4 == 0; (*equation of second plane*)
eq1 = Simplify[Inner[Subtract, Thread[2 *p1, Equal], p2, Equal]]; (*eliminate x*)
zt = t; (*let z=t*)
yt = y /. First@Solve[eq1 /. z -> zt, y]; (*find y in terms of t*)
xt = x /. First@Solve[p1 /. {z -> t, y -> yt}, x]; (*find x in terms of t*)
Show[
Plot3D[z /. First@Solve[p1, z], {x, -2, 2}, {y, -3, 3},PlotStyle -> Green, Mesh -> None],
Plot3D[z /. First@Solve[p2, z], {x, -2, 2}, {y, -3, 3},PlotStyle -> LightBlue, Mesh -> None],
ParametricPlot3D[{xt, yt, zt}, {t, -3, 3}, PlotStyle -> {Thickness[.03], Red}], Axes -> None, Boxed -> False
]