The current entry from the Oxford Dictionary says: The plural of forum is usually spelled forums; the plural fora (as in the original Latin) is chiefly used when talking about a public square in an ancient Roman city.

Thank you very much, I will have a look at those!

I would start by detecting the edge:

img=Import[.......];
img=ImagePad[img,{{-250,0},{0,0}}];
img=ColorNegate[Binarize[img,0.5]];
img=FillingTransform[img];
img=DeleteSmallComponents[img,1000];
img=MorphologicalPerimeter[img,CornerNeighbors->False];
pos=N@PixelValuePositions[img,1];
{len,ord}=FindShortestTour[pos];
pos=pos[[ord]];


{xdata,ydata}=Transpose[pos];

(* add any smoothing function here (like moving average of lowpass filter) *)
len=Length[xdata];
xpos=Interpolation[xdata,InterpolationOrder->3];
ypos=Interpolation[ydata,InterpolationOrder->3];
ParametricPlot[{xpos[t],ypos[t]},{t,1,len}]/. Line -> Arrow

resulting in:

Now we can calculate the distance between each two points:

lens={#+1,ArcLength[{xpos[t],ypos[t]},{t,#,#+1}]}&/@Range[0,len-1];
lens=Prepend[lens,{0,0.}];
lens[[All,2]]=Accumulate[lens[[All,2]]];
ListPlot[lens]

Resulting in:

Now inverting the function and evaluating some 'times':

inverselens = Reverse /@ lens;
inverselens = Interpolation[inverselens];
times = inverselens /@ Subdivide[1, Max[lens[[All, 2]]], 100];
Graphics[Point[Table[{xpos[t], ypos[t]}, {t, times}]]]

I am not sure what level of uniformity you need, but here are some thoughts. Import image:

i = Import["https://wolfr.am/emNdJOkT"];

Check the size:

ImageDimensions[i]

{1288, 1024}

Perform a set of operation to get single-pixel-wide border:

iEdge = DeleteSmallComponents[Pruning[Thinning[
    Dilation[ColorNegate[Binarize[ImageTake[i, {1, -1}, {250, -1}]]], 2]]]]

Get the coordinates of the pixels and sort them in the order that goes along the border:

pts = #[[FindShortestTour[#][[2]]]] &@PixelValuePositions[iEdge, 1];
ListPlot[pts, AspectRatio -> Automatic, PlotTheme -> "FrameGrid"]

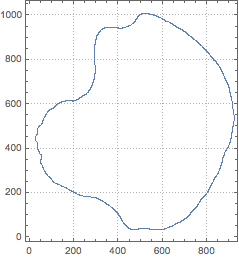
You could stop here, because perhaps this is uniform enough? If not you can a get true uniformity by getting analytic expression for the curve:

spln = BSplineFunction[pts]

Then use a trick of automatic even mesh:

ParametricPlot[spln[t], {t, 0, 1},

 (*the trick*)
 Mesh -> 30,
 MeshFunctions -> {"ArcLength"},

 (*styles*)
 MeshStyle -> Directive[Red, PointSize[.02]],
 MeshShading -> {Red, Blue},
 PlotTheme -> "FrameGrid",
 AspectRatio -> Automatic]

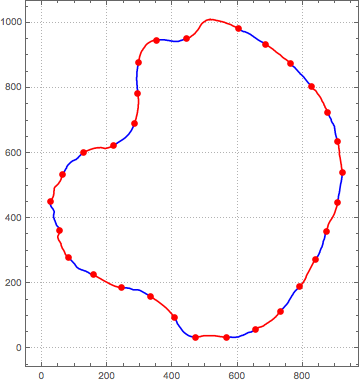
You can get mesh coordinates as:

raw = ParametricPlot[spln[t], {t, 0, 1},
   Mesh -> 20,
   MeshFunctions -> {"ArcLength"},
   MeshStyle -> Red];
allPoints = Cases[raw, x_GraphicsComplex :> x[[1]], Infinity][[1]];
meshIndex = Cases[raw, {RGBColor[1, 0, 0], Point[x_]} -> x, Infinity][[1]];
allPoints[[meshIndex]]

Thank you so much for your detailed reply, I will have a go at that and see how it works, but it definitely looks like what I am going to need!

Evenly spaced as in distance along the perimeter, apologies for not clarifying that earlier!