I am not sure what level of uniformity you need, but here are some thoughts. Import image:
i = Import["https://wolfr.am/emNdJOkT"];
Check the size:
ImageDimensions[i]
{1288, 1024}
Perform a set of operation to get single-pixel-wide border:
iEdge = DeleteSmallComponents[Pruning[Thinning[
Dilation[ColorNegate[Binarize[ImageTake[i, {1, -1}, {250, -1}]]], 2]]]]
Get the coordinates of the pixels and sort them in the order that goes along the border:
pts = #[[FindShortestTour[#][[2]]]] &@PixelValuePositions[iEdge, 1];
ListPlot[pts, AspectRatio -> Automatic, PlotTheme -> "FrameGrid"]
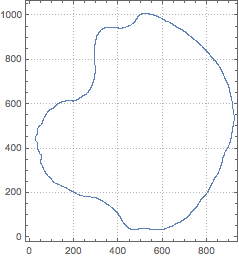
You could stop here, because perhaps this is uniform enough? If not you can a get true uniformity by getting analytic expression for the curve:
spln = BSplineFunction[pts]

Then use a trick of automatic even mesh:
ParametricPlot[spln[t], {t, 0, 1},
(*the trick*)
Mesh -> 30,
MeshFunctions -> {"ArcLength"},
(*styles*)
MeshStyle -> Directive[Red, PointSize[.02]],
MeshShading -> {Red, Blue},
PlotTheme -> "FrameGrid",
AspectRatio -> Automatic]
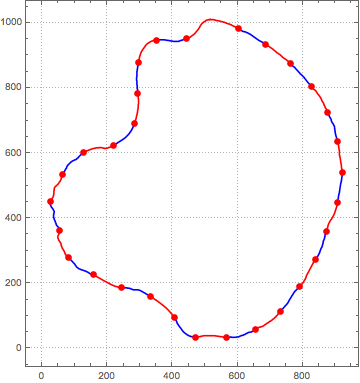
You can get mesh coordinates as:
raw = ParametricPlot[spln[t], {t, 0, 1},
Mesh -> 20,
MeshFunctions -> {"ArcLength"},
MeshStyle -> Red];
allPoints = Cases[raw, x_GraphicsComplex :> x[[1]], Infinity][[1]];
meshIndex = Cases[raw, {RGBColor[1, 0, 0], Point[x_]} -> x, Infinity][[1]];
allPoints[[meshIndex]]