Message Boards Message Boards

[GIF] Drumbeat (Vibration mode of a circular drum)

Vibration mode of a circular drum

Drumbeat

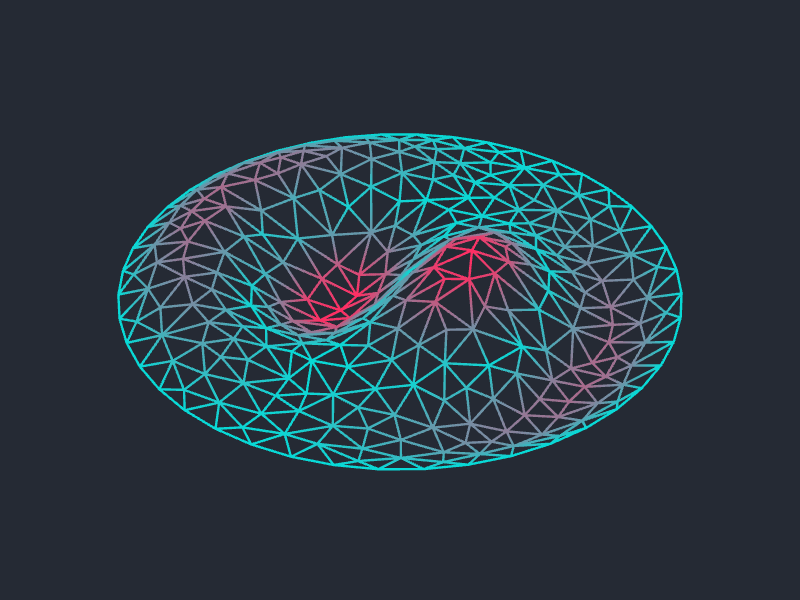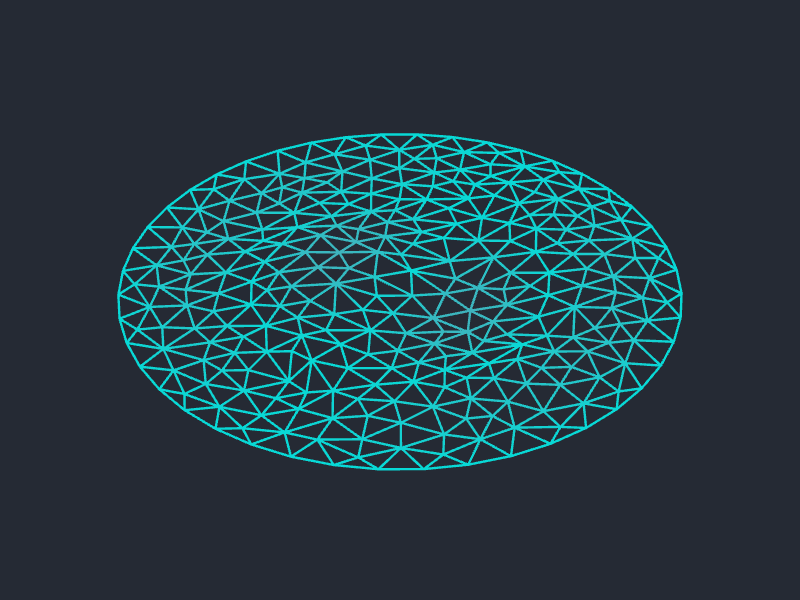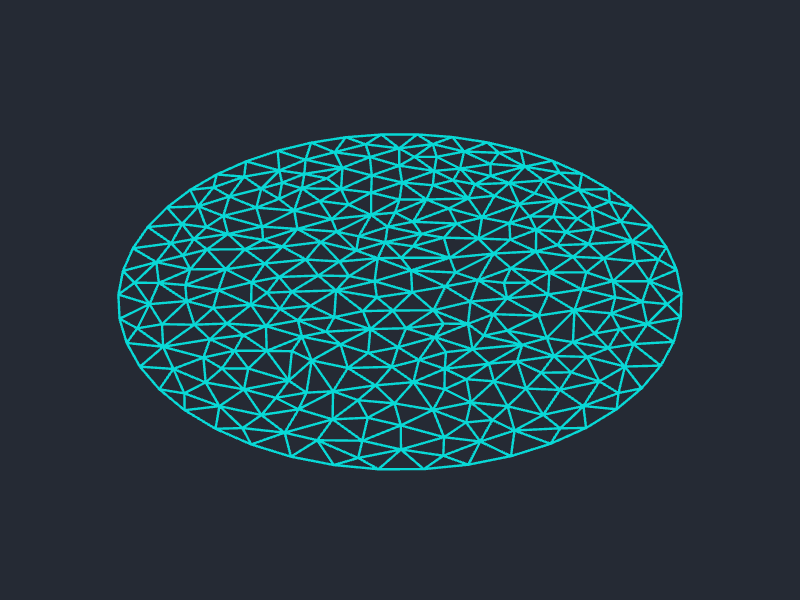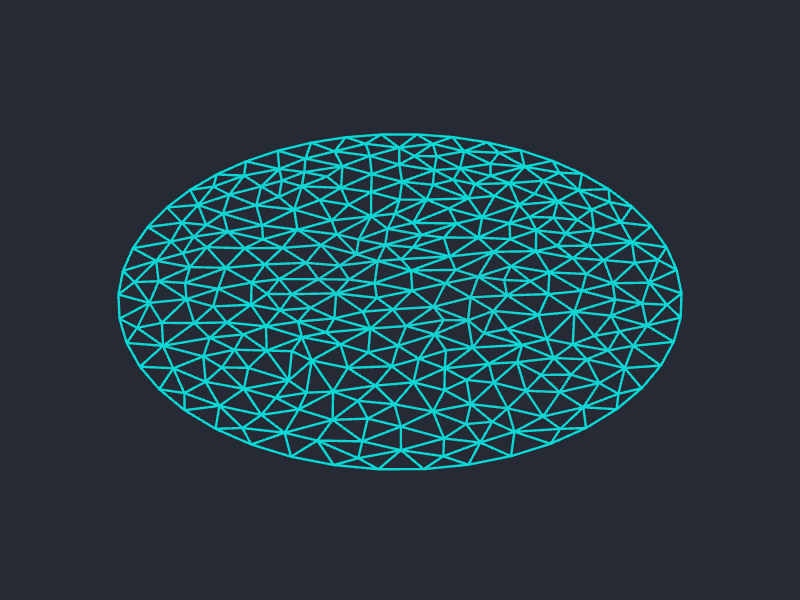
Inspired by a comment made by @J. M. on Square Up, this is an animation showing the (1,2) vibrational mode of a circular drum. I've added a (quite possible completely unphysical) exponential decay term, just because.

As you can see on the Wikipedia page, the $(m,n)$ vibrational mode of a circular membrane is given, as a function whose input is the position and whose output is the (vertical) displacement from the rest state, by

$ u_{mn} (r,\theta,t) = (A \cos c \lambda_{mn} t + B \sin c \lambda_{mn} t) J_m(\lambda_{mn} r) (C \cos m\theta + D \sin m \theta)$,

where $\lambda_{mn}$ is the $n$th root of the Bessel function $J_m$, $c$ is a constant giving the speed of wave propogation, and $A$, $B$, $C$, and $D$ are constants.

This is of course easy enough to define, especially since Mathematica has a handy BesselJZero function:

BesselZeros = N@Table[BesselJZero[m, n], {m, 0, 5}, {n, 1, 5}];
?[m_, n_] := BesselZeros[[m + 1, n]];
u[m_, n_, r_, ?_, t_, c_, A_, B_, C_, D_] :=
  (A Cos[c ?[m, n] t] + B Sin[c ?[m, n] t]) 
    BesselJ[m, ?[m, n] r] (C Cos[m ?] + D Sin[m ?]);

So then I just took an (automatically generated) triangulation of the disk and evaluated the above function u (with various more or less arbitrary choices of parameters) on the vertices. Here's the code:

DynamicModule[
 {m = 1,
  n = 2,
  k = 3,
  c = 5,
  cols, mesh, planarverts, drumverts, lines, cl},
 cols = RGBColor /@ {"#08D9D6", "#FF2E63", "#252A34"};
 mesh = DiscretizeRegion[Disk[], MaxCellMeasure -> .009];
 planarverts = MeshCoordinates[mesh];
 lines = MeshCells[mesh, 1];
 Manipulate[
  drumverts = Append[#, 1.5 E^(-k t) u[m, n, Norm[#], ArcTan[#[[1]], #[[2]]], t, c, 1/2, 0, 1/2, 0]] & /@ planarverts;
  cl = Blend[cols[[;; 2]], Abs[#[[3]]]/.2] & /@ drumverts;
  Graphics3D[
   GraphicsComplex[
    drumverts,
    {Thickness[.004], Append[#, VertexColors -> Automatic] & /@ lines},
    VertexColors -> cl
    ],
   PlotRange -> 1, Boxed -> False, Axes -> None, 
   ImageSize -> {540, 405}, ViewAngle -> ?/10, 
   ViewCenter -> {1/2, 1/2, .46}, Background -> cols[[-1]]
   ],
  {t, 0., 2 ?/?[m, n]}]
 ]
POSTED BY: Clayton Shonkwiler
6 Replies
Sort By:

Here's a fun but less pretty related topic: https://mathematica.stackexchange.com/a/158416/5478
POSTED BY: Kuba Podkalicki

IIRC, the exponential decay is ‘physical’—and you can also Play the sound the drum makes!

But this actually only makes sense if you include the most appropriate “harmonics”—actually, the superposition of various modes, given different weightings, and different decay rates—which have frequencies that are not rational multiples of one another!

I did this a few years ago (before the Community existed), using measured values for the weightings and decay rates—from The Physics of Musical Instruments—and the sound generated was a reasonable approximation to a Timpani or Kettle Drum (but, of course, the body of the drum is actually a key to the sound generated). Here is an example:

Play[1.0 Cos[128 2 Pi t] E^(-((5.25 t)/0.4)) + 
  2.5 Cos[145 2 Pi t] E^(-((5.25 t)/2.3)) + 
  1.9 Cos[218 2 Pi t] E^(-((5.25 t)/3.7)) + 
  1.5 Cos[287 2 Pi t] E^(-((5.25 t)/4.6)) + 
  0.7 Cos[354 2 Pi t] E^(-((5.25 t)/4.3)), {t, 0, 2}]

And there is also NDEigensystem, which I recently used to try out the “hearing the drum” problem (again I need to find this, and post it!)
POSTED BY: Paul Abbott

"Can One Hear the Shape of a Drum?" is the title of a 1966 article by Mark Kac. The study of vibrations on drums led mathematicians to pose a famous mathematical problem on whether the shape of a drum can be heard, with an answer arriving only in 1992. The frequencies at which a drumhead can vibrate depend on its shape. A central question is the reverse problem -- whether the shape can be predicted if the frequencies are known. Kac did not know if it was possible for two different shapes to yield the same set of frequencies. The question was finally answered in the early 1990s by Gordon, Webb and Wolpert. And... You Can't Always Hear the Shape of a Drum :-) On the photo: David Webb and Carolyn Gordon with paper models of a pair of "sound-alike" drums. See also PBS video: https://youtu.be/N3qmN6pYhi0

enter image description here

Photo courtesy of Washington University Photographic Services
POSTED BY: Vitaliy Kaurov

Yes, I definitely started with a polar mesh, but it wasn't quite working for me, so I went for something a little more asymmetrical.
POSTED BY: Clayton Shonkwiler

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations !

We are happy to see you at the top of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: Moderation Team
J. M.
J. M.
Posted 8 years ago

I'm glad you used the idea. :) Normally I'd use a polar mesh to depict this, but I think the triangulated circle looks great here. Makes it look like a funky trampoline.
POSTED BY: J. M.
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract