Message Boards Message Boards

3
|
6222 Views
|
3 Replies
|
8 Total Likes
View groups...
Share
Share this post:

Improve cryptanalysis by beginner

Luis Ledesma
Posted 9 years ago

Hello everyone, I decided long ago to solve the exercise to propose on page rosetta code, here is the link, the way I solved it was this (see attached file) ,

My code

I think there is a shorter way to do this but still can not find it, if any of you can help me have a more efficient code would be of much help, greetings and thanks in advance

Attachments:
POSTED BY: Luis Ledesma
3 Replies
Sort By:

The code can be simplified slightly (note that I use StringPart which is a new V11 function):

cifrado=StringDelete[txt," "|"\n"];
trig=StringPartition[cifrado,3,1];
rep=Tally[trig];
cant=Select[rep,#[[2]]>1&];
posci=Flatten[Position[trig,#]]&/@cant[[All,1]];
dista=Flatten[Differences/@posci];
descom=Tally[Flatten[FactorInteger[dista],1]];
fin=SortBy[descom,Last];
pana=Table[StringPart[cifrado,k ;; ;; 14],{k,14}]
conv=Table[Count[w,#]&/@CharacterRange["A","Z"],{w,pana}];
gt=Mod[Table[i + {0, 4, 14, 19}, {i, 0, 25}], 26];
colconv=Table[Total[k[[#+1]]]&/@gt,{k,conv}];
CharacterRange["a","z"][[Flatten[Position[#,Max[#]]&/@colconv]]];

Optimisations are:

  • Using StringDelete rather than StringSplit/StringJoin
  • largo is not needed any more
  • trig is done using StringPartition
  • posci the Part is moved outside the Map, [[All,1]] rather than [[1]]
  • fin is done using SortBy
  • pana is done using StringPart
  • pana the starting iterator 1 is not needed
  • conv, rather than iterating over an index, iterate directly over pana
  • gt is calculated cleaner (and faster)
  • colconv, rather than iterating over an index, iterate directly over conv

Most are cleaner, and faster modifications, I didn't fully understand the method to be honest, so I just looked at the code in an abstract way...
POSTED BY: Sander Huisman

This is not bad at all. I'd make modest changes to the first several lines, as below.

cifrado = StringJoin[StringSplit[txt]];
largo = StringLength[cifrado];
trig = StringPartition[cifrado, 3, 1];
rep = Tally[trig];
cant = Select[rep, #[[2]] > 1 &];
posci = Position[trig, #[[1]]] & /@ cant;
dista = Flatten[Differences[#] & /@ posci];
dists = Sort[Tally[dista]]

(* Out[1008]= {{14, 1}, {42, 5}, {48, 1}, {56, 13}, {87, 1}, {98, 
  1}, {126, 4}, {130, 1}, {168, 3}, {196, 1}, {238, 1}, {252, 
  1}, {259, 2}, {266, 1}, {294, 1}, {316, 1}, {322, 1}, {376, 
  1}, {401, 1}, {403, 1}, {420, 1}, {479, 1}, {524, 1}, {580, 
  1}, {583, 1}, {714, 1}, {805, 1}} *)

From here, your use of FactorInteger I think is good. I do not see exactly how you then deduce 14 as a candidate period, though I can think of ways that could happen, so maybe that part needs elaboration. An alternative might be to do an irregular Fourier transform.

dft[w_?NumberQ, gaps_, lens_] := Total[Exp[I*w*gaps]*lens]

Plot[Abs[dft[w, periodmults, dists[[All, 2]]]], {w, 0, 3}, 
 PlotRange -> All, PlotPoints -> 300]

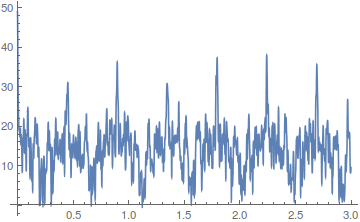
enter image description here

If you home in on the first two peak frequencies, you will find that they are near .454 and .898. 2*Pi/peak gives very close to 7 and 14. Also if you clip all repeated triads that have fewer than three appearances, the signal for period 14 improves somewhat.
POSTED BY: Daniel Lichtblau

Should not it be here? Rosetta Code Challenge & Wolfram Language

POSTED BY: Vitaliy Kaurov
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract