Hi Ed,

I am not sure what exactly what you want to achieve. This is what I think you want. I will demonstrate it with a list of only 4 elements.

Rule[#, 0] & /@ # & /@ Subsets[Table[Subscript[\[Theta], i], {i, 0, 4}]]

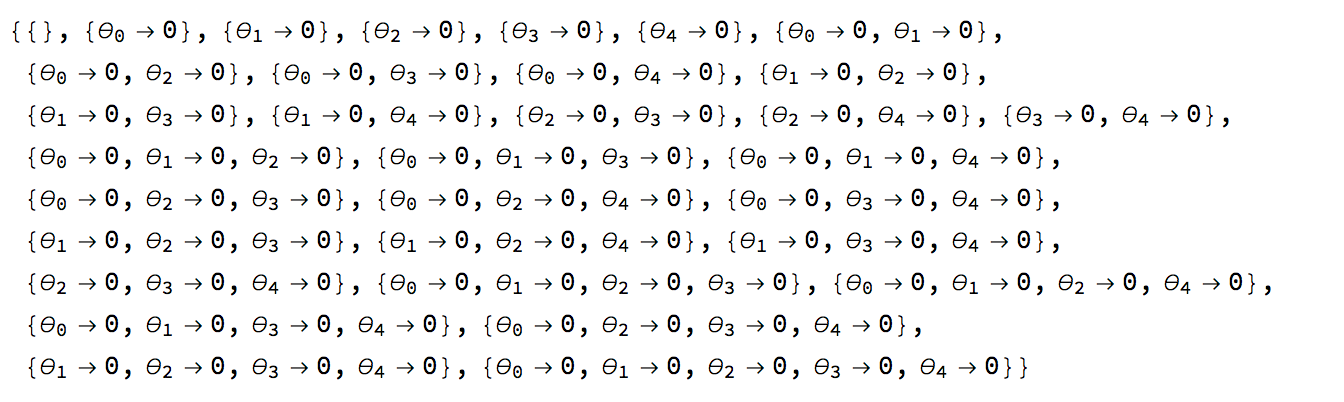
So you first have a list where nothing is set to zero, then four lists where each of the elements is set to zero, then lists where all combinations of 2 elements are set to zero, etc.

If you actually want the lists this might work.

(Table[Subscript[\[Theta], i], {i, 0, 4}] /. #) & /@ (Rule[#, 0] & /@ # & /@ Subsets[Table[Subscript[\[Theta], i], {i, 0, 4}]])

Things like these might also work:

ReplacePart[Table[Subscript[\[Theta], i], {i, 0, 4}], Rule[#, 0] & /@ #] & /@ Subsets[Range[4]]

or

ReplacePart[Evaluate[Table[Subscript[\[Theta], i], {i, 0, 4}]], Flatten[Outer[Rule, #, {0}]]] & /@ Subsets[Range[4]]

This could certainly be made more elegant and faster, but for your 16 elements it is quite fast anyway.

AbsoluteTiming[rules = Rule[#, 0] & /@ # & /@ Subsets[Table[Subscript[\[Theta], i], {i, 0, 16}]];]

This evaluates in under one second.

Cheers,

M.

Perhaps this version is easier to get the hang of:

Subsets[Table[Subscript[\[Theta], i] -> 0, {i, 5}]]

A Rest will get rid of the the meaningless empty rule set:

Rest@Subsets[Table[Subscript[\[Theta], i] -> 0, {i, 5}]]

Yes, that is much more direct and elegant ....

Dear Ed,

well, yes your program does certainly do that. The Apply function is mapped onto each element of the list, i.e. onto each sublist. Then you total everything. You can get the same effect with this:

Total[Times @@@ Subsets[Table[Subscript[\[Theta], i], {i, 5}]]]

The LeafCount of both solutions is the same; mine's just a shorthand of yours. On the other hand, if that is what you want to achieve, then this might work, too:

Det[DiagonalMatrix[Table[1 + Subscript[\[Theta], i], {i, 6}]]] // Expand

Interestingly, that allows you to get yet another answer to your first question:

List @@ Expand[Det[DiagonalMatrix[Table[1 + Subscript[\[Theta], i], {i, 6}]]]]

This would have been my preferred solution for aesthetic reasons, but I somehow doubt, that this would have made my initial reply clearer.

Consider also this:

Cheers, M.

PS: Interestingly,

Expand[Product[1 + Subscript[\[Theta], i], {i, 16}]]

is not faster; I would have expected this to be faster than the matrix thing.

Hi Ed,

this

Select[Subsets[Table[Subscript[\[Theta], i], {i, 5}]], FreeQ[#, Subscript[\[Theta], 3]] \[And] FreeQ[#, Subscript[\[Theta], 4]] &, Infinity]

or

Select[Subsets[Table[Subscript[\[Theta], i], {i, 5}]], ContainsOnly[#, Complement[Table[Subscript[\[Theta], i], {i, 5}], {Subscript[\[Theta], 3], Subscript[\[Theta], 4]}]] &]

might work. Of course if that is what you want you can directly use:

Subsets[Complement[Table[Subscript[\[Theta], i], {i, 5}], {Subscript[\[Theta], 3], Subscript[\[Theta], 4]}]]

Cheers,

Marco

I forgot to mention that what I needed it is the opposite of the outcome of the commands above but thanks to your answer I have one solution at least

Select[Subsets[Table[Subscript[\[Theta], i], {i, 5}]], 
 MemberQ[#, Subscript[\[Theta], 3]] \[And] 
   MemberQ[#, Subscript[\[Theta], 4]] &, Infinity]

Many thanks

Ed

Dear Marco

Many thanks. Please correct me if I am wrong but in the solution you have just posted I have to remember the thetas not involved in the first part, {1,2,5}, and that could be difficult when I have, say, 16 instead of 5, right?

I have another question but I think it should be posted in another thread.

Again thank you very much for your help and patience.

regards

Ed